Klirrfaktor - wie viel ist zu viel?
Musikhören ist eine höchst emotionale Angelegenheit. Damit die Wiedergabe so naturgetreu wie möglich ist wird viel gemessen, d.h. das Sollsignal wird mit dem Istsignal verglichen. Objektive Messung und subjektive Beurteilung sollten im Idealfall zusammen passen. Beim Frequenzgang klappt das noch ganz gut, beim Klirrfaktor aber schon nicht mehr. Während man bei Verstärkern 0.01 % Klirrfaktor bemängelt sollen bei Lautsprechern 3% im Bassbereich "nicht so schlimm" sein?
Der folgende Artikel soll etwas Licht ins Klirrdunkel bringen. Wer will kann sein Klirrhörvermögen auch mit einem kleinen Progrämmchen "blind" testen . . .
- Öffentliche Version des Artikels
- Version für Abonnenten
Klirrfaktor - wie viel ist zu viel?
Musikhören ist eine höchst emotionale Angelegenheit. Damit die Wiedergabe so naturgetreu wie möglich ist wird viel gemessen, d.h. das Sollsignal wird mit dem Ist-Signal verglichen. Objektive Messung und subjektive Beurteilung sollten im Idealfall zusammen passen. Beim Frequenzgang klappt das noch ganz gut: möglichst linear soll er halt sein. Dann gibt es da aber noch so Sprüche wie "Überhöhungen sind schlimmer als Einbrüche", da fängt die Kaffeesatzleserei schon an.
Bei anderen Dingen klappt das noch weniger, wie z.B. bei den sogenannten "nichtlinearen Verzerrungen" wie Klirrfaktor (das System antwortet auch mit X · Anregungsfrequenz) oder Intermodulationsverzerrungen (Mischfrequenzen bei Anregung mit mehreren Signalen). Da heißt es dann z.B.:
- die harmonischen Verzerrungen K2 stören weniger (= dürfen also höher sein). Schließlich sind sie genau 1 Oktave höher als das Anregungssignal und integrieren sich daher besser (= harmonischer) in die Musik.
- da sich K3 weniger harmonisch in die Musik integriert stören schon kleinere Mengen davon - aber wie viel?
- ach ja, und im Bassbereich darf es ruhig etwas mehr Klirrfaktor sein, denn da stört er kaum sondern erhöht z.T. noch die "gefühlte" Lautstärke
Gar nicht so einfach, oder? Aber ab wann ist denn nun ein bestimmter Klirrfaktor Kx störend, und ist das ggf. sogar noch von der Wiedergabelautstärke abhängig? Fragen über Fragen, aber keine konkreten Antworten. Warum ist das denn so schwierig?
Das Ohr ist kein Mikrofon
Unser Hörempfinden (d.h. der Weg vom Außenohr bis zum Gehirn) ist leider nicht ganz so linear wie ein gutes Mikrofon sondern in vielerlei Hinsicht "komisch". Dieses auf den ersten Blick "komische" Verhalten hat sich aber in der Evolution als vorteilhaft erwiesen - und deswegen haben wir es geerbt.
Bei mittleren Frequenzen sind wir z.B. sehr empfindlich, da es für das Überleben sehr hilfreich war, wenn man das nicht ganz lautlose Anschleichen einer urzeitlichen Raubkatze am leisen Knacken eines Zweiges erhören und damit früh genug flüchten konnte. Deshalb sind wir auch für tiefe Frequenzen wie Donnergrollen oder das Stampfen der Füße auf dem Waldboden unempfindlicher (sehr zum Leidwesen der Surroundfraktion, die die lauten tiefen Töne nur mit hohem Aufwand reproduzieren kann).
Wenn man die subjektiv empfundene Lautstärke - auch Lautheit genannt - gegenüber der objektiv messbaren Lautstärke aufträgt erhält man folgendes Bild:
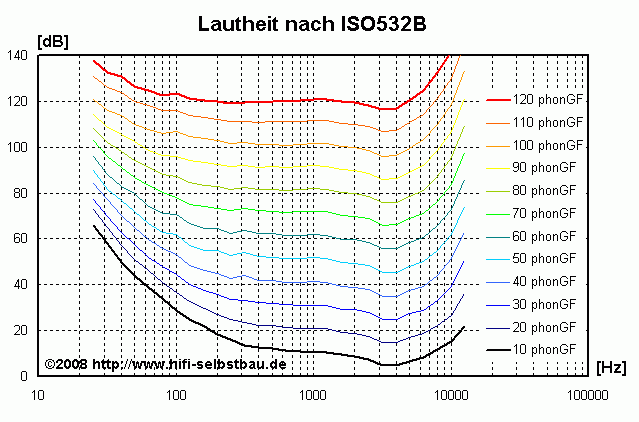
Wie liest man diese Grafik? Die einzelnen Kurven sind Isophone, d.h. Kurven gleich empfundener Lautheit. Sie haben die Einheit Phon (der Zusatz GF bedeutet, dass eine Freifeldausbreitung angenommen wurde). Fangen wir bei der schwarzen Kurve an. Einen gemessenen Schalldruck von 10 dB bei 1000 Hz empfindet man subjektiv so laut wie 10 Phon. Bei 100 Hz muss man schon einen objektiven Schalldruck von 29 dB erzeugen damit er genau so laut empfunden wird wie die 10 dB bei 1000 Hz. Beide Punkte liegen auf der schwarzen Kurve, der 10 Phon-Kurve.
Dass das wirklich so ist kann man sehr gut nachvollziehen, wenn man einen Sinuston mit konstanter Amplitude von 20 bis 20000 Hz durchstimmt und das Ergebnis über einen guten Kopfhörer abhört. Das obere Bild zeigt das Zeitsignal (immer 50% Vollaussteuerung), das untere die Frequenzanalyse:
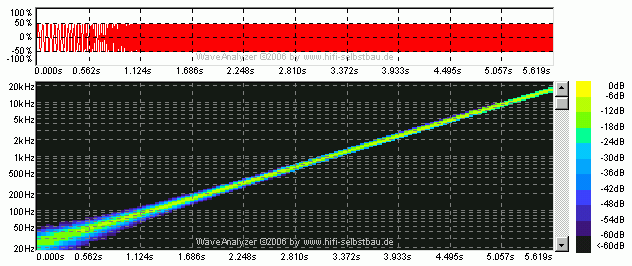
-> Obwohl der objektive Pegel immer gleich bleibt sind die tiefen Töne kaum zu hören während es im mittleren Freqenzbereich unangenehm laut wird
Hinweis: Abonnenten könnten sich das Signal jetzt anhören
Signal als MP3-Datei (45 kB)
Der Verlauf der Isophonen ist leider sehr "krumm", so dass man in der Vergangenheit ein einfaches analoges Filter gesucht hat, welches dieses Verhalten möglichst gut annähert. Da das nicht für den gesamten Lautstärkebereich geht hat man verschiedene Bewertungs-Filter für verschiedene Lautstärkeschwerpunkte entwicklet:
- die A-Bewertung für kleinere bis mittlere Lautstärken
- die B-Bewertung für mittlere bis hohe Lautstärken
- die D-Bewertung für hohe bis sehr hohe Lautstärken (Flugzeuglärm)
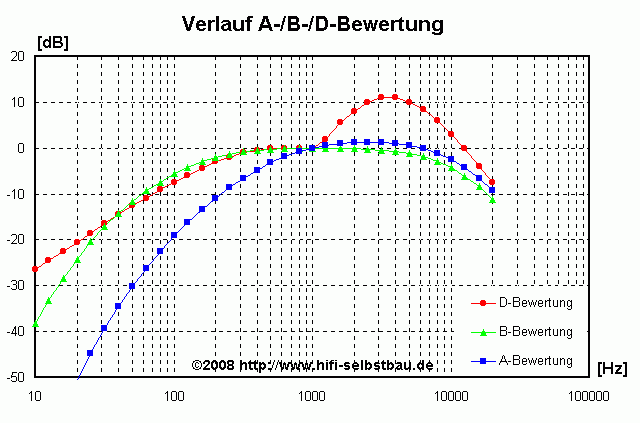
Die inversen Bewertungsfilter müssten also idealerweise genau so verlaufen wie die Phonkurve im Bereich der "Ziellautstärke":
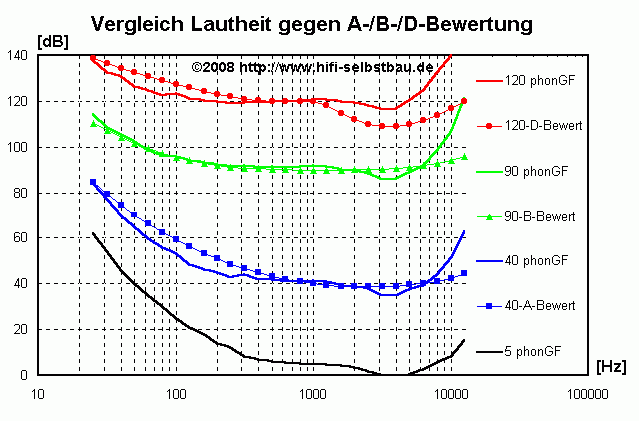
Na ja, so ganz kommt das für die A- und D-Bewertung nicht hin, aber die Kurve "90 dB - B-Bewertung" stimmt recht gut mit der 90 Phon-Kurve überein. Was würde denn das für den Klirrfaktor bedeuten? Am deutlichsten wird das bei der A-Bewertung:
- Wenn man einen Ton mit einem Schalldruckpegel von 75 dB bei 40 Hz erzeugen würde und der Lautsprecher einen Klirrfaktor K2 von 10 % hätte, dann entspräche dies einem Ton von 80 Hz mit einem Schalldruckpegel von 55 dB
- Da man für Töne von 80 Hz aber (laut A-Bewertung) 12.1 dB empfindlicher wäre würde ich den Klirrfaktor 4x lauter empfinden als er physikalisch ist, also wie 40%
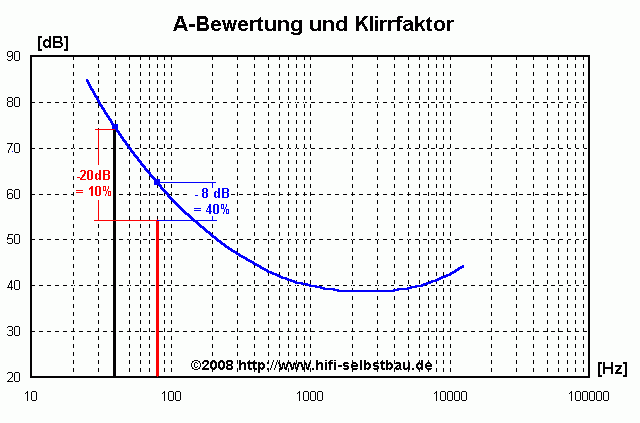
Wenn dies der relevante subjektive Faktor wäre würde dies bedeuten, dass der Klirrfaktor im Bassbereich subjektiv kritischer ist als es objektiv den Anschein hätte. Dummerweise gibt es gerade bei kleineren Lautsprecherchassis (z.B. 10 cm Durchmesser) auch noch jede Menge Klirrfaktor in diesem Bereich bei diesem Pegel. Dies entspricht aber nicht der "Erfahrung" die besagt, dass der Klirrfaktor im Bassbereich eher unkritischer ist. Was könnte es denn sonst sein?
Zwicker sei Dank
In den 50er und 60er Jahren tat sich besonders die TU München/Prof. Zwicker mit Studien zum Thema Lautheitsempfinden hervor (s. Liste der Veröffentlichungen). E. Zwicker und R. Feldtkeller haben ihre Erkenntnisse zu dem Thema 1967 u.a. im Buch Das Ohr als Nachrichtenempfänger zusammengefasst. Diese Untersuchungen führten schließlich zu einem genormten Verfahren der Lautheitsberechnung (DIN 45631 bzw. ISO 532B).
Es wurde festgestellt, dass bei dominanter Anregung eines schmalen Frequenzbereichs leisere Pegel in benachbarten Frequenzbereichen nicht mehr wahrgenommen werden konnten. Bei Frequenzen unterhalb des Anregungsbereiches ist dieser Effekt nur sehr schwach ausgeprägt, bei Frequenzen oberhalb des Anregungsbereiches hingegen ist der Effekt deutlich größer und erstreckt sich je nach Anregungspegel und Frequenz über einen weiten Frequenzbereich. Diesen Effekt nennt man spektrale Verdeckung und er wird z.B. auch bei der MP3-Datenkompression ausgenutzt.
Wenn man z.B. einen Sinuston mit der Amplitude 5% von 200 bis 5000 Hz durchstimmt und einen konstanten Sinuston von 1000 Hz mit der Amplitude 50% überlagert "verschwindet" der Gleitsinus in der Nähe des festen Tons:
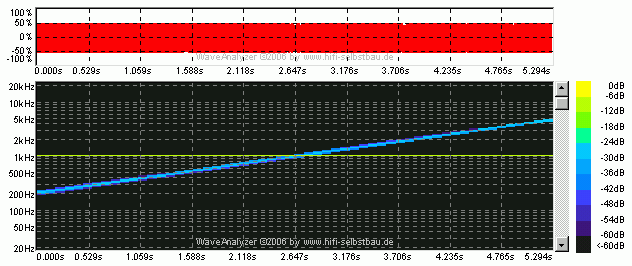
Hinweis: Abonnenten könnten sich das Signal jetzt anhören
Signal als MP3-Datei (42 kB)
Zwicker und Feldtkeller haben eine grafische Methode zu Bestimmung der Lautheit unter Berücksichtigung der spektralen Verdeckung entwickelt. So ein Diagramm sieht absolut faszinierend aus, ist aber nur sehr zeitaufwändig auszuwerten.
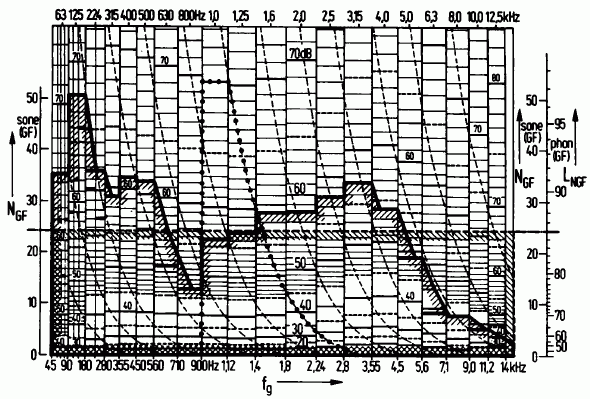
Bereits 1972 wurde daher in der Fachzeitschrift ACUSTICA ein Berechnungsprogramm vorgestellt und im Quellcode abgedruckt, welches die der grafischen Auswertung zugrunde liegenden Effekte umsetzte. Die angesagte Programmiersprache in der Zeit war FORTRAN, die Schalldruckwerte wurden über Lochkarten eingespeist.
In der DIN 45631 Stand März 1991 wurde eine aktualisierte Form des Berechungsprogramms (diesmal in QBASIC) veröffentlicht, welches erneut im Quellcode abgedruckt wurde. Dadurch konnte gewährleistet werden, dass sowohl selbst geschriebene als auch kommerzielle Programme bei gleichen Schalldruckspektren zu gleichen Ergebnissen führten. Unter Verwendung dieses Programms wurde die oben gezeigten Phonkurven berechnet. Der Schalldruckpegel in einer Terz wurde so lange erhöht, bis der berechnete Phonwert dem gewünschten Phonwert entsprach. Alle anderen Terzen wurden dabei auf -60 dB gesetzt, so dass sie nicht zur Gesamtlautheit beitrugen.
| Von Oktaven, Terzen und Dekaden? (nur für technisch Interessierte) |
| Verdoppelt man die Anregungsfrequenz von F auf 2 · F so ist der neue Ton eine Oktave höher
-> Oktave = Verfrequenzänderung um den Faktor 2 Da so große Frequenzverhältnisse in der technischen Akustik nicht immer ausreichen wird die Oktave oft in n prozentual gleich große Bereiche unterteilt (z.B. 1/n-Oktavanalyse). Üblich sind 1/3-, 1/6- und 1/12-Oktavschritte. Ein 1/3-Oktavschritt entspricht etwa einer musikalischen Terz (3-Ton-Intervall). Daher wird der Begriff "Terz" in der technischen Akustik stellvertretend für einen 1/3-Oktavschritt verwendet. Nach DIN 45562 lauten die Terzmittenfrequenzen ausgehend von 1000 Hz wie folgt: 315, 400, 500, 630, 800, 1000, 1250, 1600, 2000, 2500, 3150 Hz etc. Der Abstand der Mittenfrequenzen beträgt 2(1/3) bzw. 126%. |
Man kann damit aber auch die im Programm realisierte spektrale Verdeckung "herauskitzeln". Dazu gibt man die dominante Anregung in einer Terz vor und berechnet deren Lautheit (alle anderen Terzbänder wurden wieder zu -60 dB gesetzt). Dann wurden einzelne Terzbänder so lange erhöht, bis sich die Gesamtlautheit gerade um 1/100 Phon erhöht hat. Wenn man das bei einer Anregungsfrequenz von 1 kHz bei verschiedenen Pegeln macht ergibt sich folgendes Bild:
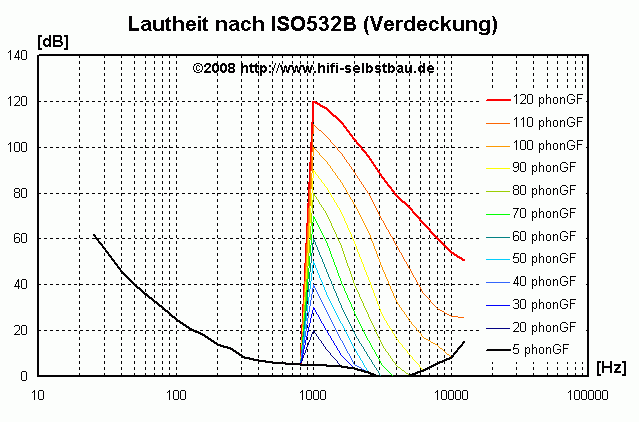
- Das Programm berücksichtigt offenbar keine spektrale Verdeckung zu tieferen Frequenzen
- Die spektrale Verdeckung zu höheren Frequenzen ist bei höheren Pegeln sehr hoch
Am Beispiel einer Anregung von 90 dB bei 1 kHz kann man die "verdeckten" Klirrfaktoren schön sehen:
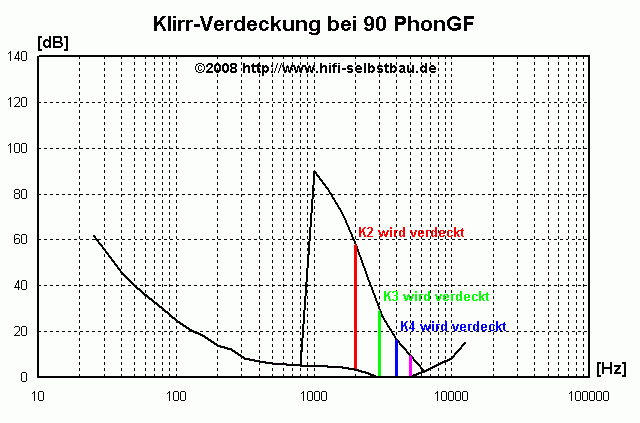
Wenn man dies für alle Anregungsfrequenzen und alle Pegel macht und den Pegel der Klirrfaktoren in Bezug setzt zum Anregungspegel kann man für jede Harmonische getrennt ein Kennlinienfeld erstellen:
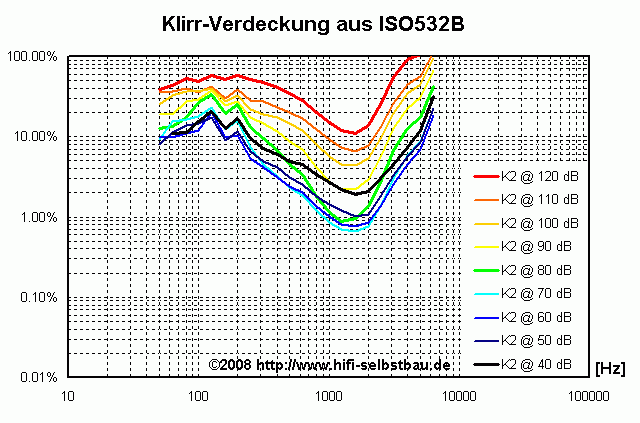
Hinweis: Abonnenten könnten nun weitere Kennlinienfelder für K3 bis K12 sehen
Selbst ist der Mann
Wer das nicht glaubt kann es gerne selber ausprobieren. Dazu haben wir ein kleines Progrämmchen (35 kB, muss nicht installiert werden) geschrieben, mit dem man bei wählbarer Grundfrequenz verschiedene Dosen von Klirrfaktor beimischen kann.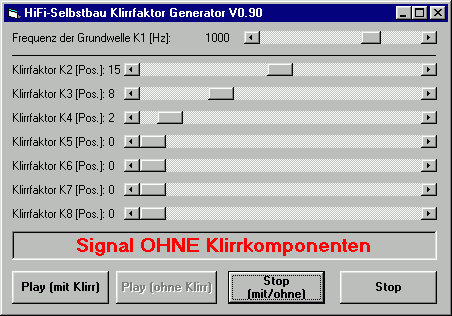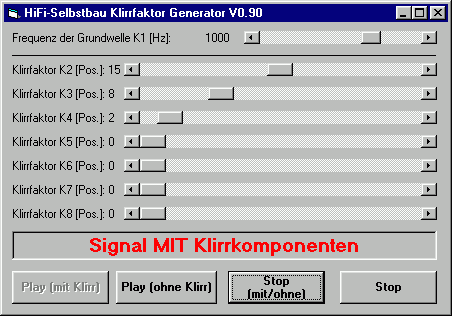
Durch abwechselndes Spielen der Variante ohne und mit Klirrfaktor kann mehr sehr schön den Punkt finden ab dem sich der Klangcharakter ändert. Damit dies ein Blindtest ist wurde die Skala nicht beschriftet und die Skalen für die verschiedenen Klirrfaktoren haben in der Regel unterschiedliche Einteilungen. Beim Start des Programms gibt es einen kurzen Hinweis für die Vorgehensweise:
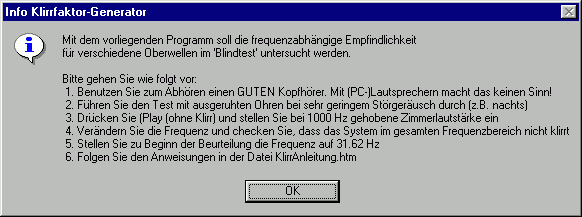
Programm für Abonnenten mit Anweisungen etc. (ZIP-Datei, 18 kB)Hinweis: Sollte die Datei Msvbvm50.dll nicht im WINDOWS-Verzeichnis (z.B. C: \ WINDOWS \ SYSTEM) vorhanden sein kann man sie z.B. hier downloaden (686kB).
Fazit:
Durch konsequente Anwendung einer genormten Rechenvorschrift konnte für einen breiten Anregungspegelbereich für verschiedene Klirrkomponenten der "erlaubte" (weil unhörbare) Klirrfaktor bestimmt werden. Die Ergebnisse korrespondieren sehr gut mit den "Faustformeln", geben aber zusätzlich quantitative Angaben. Generell gilt:- die Klirrempfindlichkeit ist im mittleren Frequenzbereich um 1 kHz am größten
- bei 100 Hz bzw. 5 kHz ist die Klirrempfindlichkeit etwa 10x kleiner
- für mittlere Pegelbereiche von 70 bis 90 dB ist die Klirrempfindlichkeit am größten
Für Abonnenten gibt es an dieser Stelle noch eine Reihe von weiterführenden Links.
Kommentare
Fazit: Der Zenit von HiFi war schon 1988 erreicht. Ab dann ging es technisch anscheinend noch aufwärts aber klanglich eher wieder abwärts.
Der PCM-Standard für CDs ist seit 1983 gesetzt und wurde dann vom MP3-Format noch unterboten - dabei sind schon 80% aller CDs schlecht aufgenommen.
Und der Begriff "High-End" hat eher die Preise in die Höhe getrieben als die objektive bzw. eher subjektive Klang-Qualität gesteigert.
Danke!