Die meisten Lautsprecher funktionieren nach dem sog. dynamischen Prinzip:
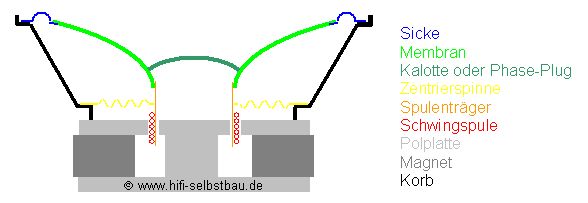
Wenn man so einen Lautsprecher vor sich liegen hat schnellt (besonders bei kleinen Kindern) unwillkürlich der Zeigefinger vor und drückt mitten auf die Membran. Dabei merkt man dann, dass der Lautsprecher der Kraft einen bestimmten Widerstand entgegensetzt, wie das auch eine Feder tun würde. Und wenn man wieder loslässt, sorgt irgendetwas am Lautsprecher dafür, dass die Membran wieder in ihre Ruhelage zurück kehrt. Für beide Effekte ist die Sicke und vor allem die Zentrierspinne verantwortlich. Beide Teile zusammen bilden die Feder des Lautsprechers.
Während der Lautsprecherkorb fest mit dem Gehäuse verbunden wird kann sich die Membran samt "Anbauteilen" dank der federnden Einspannung bewegen. Zusammen mit der Membran bewegt sich z.B. die Staubschutzkalotte sowie der Schwingspulenträger samt Schwingspule. Auch der innere Teil der Zentrierspinne und der Sicke bewegt sich mit, während der äußere Teil mit dem Korb verbunden ist und sich daher nicht bewegt. Alle diese beweglichen Teile haben natürlich auch eine Masse.
Tja, und wo eine Masse und eine Feder sind, da ist auch eine Resonanzfrequenz nicht weit! Das kann man schön mit einem kleinen praktischen Experiment nachvollziehen. Man nehme ein gewöhnliches, z.B. 30 cm langes Kunststofflineal, lege es flach auf den Tisch und lasse es z.B. 15 cm an der Tischkante überstehen. Dann drückt man den auf dem Tisch liegenden Teil des Lineal mit der flachen Hand an, drückt das freie Ende gleichzeitig z.B. 1 cm runter und lässt dann schnell los. Dann ertönt ein aus Comicfilmen bekannter Ton, der immer leiser wird und schließlich verstummt: das freie Linealende schwingt auf seiner Eigenresonanz aus. Wenn man nun nur etwa 10 cm überstehen lässt und das freie Ende wieder 1 cm runterdrückt merkt man erst mal, dass es diesmal etwas schwerer geht. Lässt man wieder schnell los, dann ertönt jetzt ein hellerer Ton -> durch die Erhöhung der Steifigkeit geht die Resonanzfrequenz nach oben.
Hätte man bei einem Überstand von 15 cm an das freie Ende des Lineals ein dickes Kaugummi (oder ein Stück Knetgummi) befestigt, dann hätte sich ein tieferer Ton ergeben -> durch die Erhöhung der Masse geht die Resonanzfrequenz nach unten.
So, damit hätten wir den mechanischen Teil des Lautsprechers erst mal verstanden. Da waren doch aber auch noch ein Terminal zum Anschluss des Verstärkersignals? Wenn man den Pluspol einer handelüblichen 1.5 Volt Batterie an die rote Markierung anschließt, bewegt sich die Membran wie durch Geisterhand bewegt nach vorne. Wenn man die Pole vertauscht geht es in die andere Richtung (so kann man z.B. auch die Polarität des Lautsprechers feststellen). Was passiert denn da? Wenn die Schwingspule mit Strom durchflossen wird, dann entsteht ein Magnetfeld um die Spule. Dieses Magnetfeld "telefoniert" mit dem Magnetfeld des Lautsprechermagneten. Je nach Polung wird die Schwingspule nun angezogen oder abgestoßen und bewegt dadurch die Membran. Je stärker der Magnet und je größer der Strom ist, desto größer ist die Auslenkung. Das funktioniert nicht nur mit einer Batterie sondern auch mit dem Ausgangsignal des Verstärkers -> Musik ertönt.
Wie kommt es denn nun zur Schallabstrahlung? Wenn sich die Schwingspule bewegt und die Membran steif genug ist, dann bewegt sich die Membran mit. Bei einer Bewegung nach vorne ergibt sich direkt vor der Membran ein ganz kleiner Überdruck, bewegt sich die Membran nach hinten ergibt sich ein ganz kleiner Unterdruck. Diese Druckänderungen bewegen sich mit Schallgeschwindigkeit von der Membran fort. Wenn sie auf unser Ohr treffen, dann hören wir den abgestrahlten Schall. Je größer die Membranfläche, desto mehr "Schallteilchen" werden bei gleicher Auslenkung angestoßen und desto mehr Schalldruck wird erzeugt.
Tja, das war's im Großen und Ganzen schon! Und was brauche ich jetzt noch, damit ich das Verhalten des Lautsprechers bei Einbau in ein geschlossenes Gehäuse berechnen kann wie das im Grundlagenartikel "geschlossene Gehäuse" beschrieben wurde? Nun, solche Dinge wie Feder, Masse, Resonanzfrequenz, Stärke des Magneten und Größe der Membran sind uns ja eben schon über den Weg gelaufen, aber wie bringt man die alle zusammen.
Man müsste die elektrischen, mechanischen und akustische Größen in ein elektrisches Schaltbild überführen können (dafür gibt es in der Physik Umformungsregeln) und dann wissen, wie man die einzelnen Parameter bestimmt. Hört sich kompliziert an, ist aber Dank den Herren Thiele und Small gar nicht soooo schlimm. Sie haben gezeigt, wie man durch einfache Impedanzmessungen diese Parameter bestimmen kann.

In Anerkennung dieser Großtat werden diese Parameter in Insiderkreisen daher Thiele-Small-Parameter (oder kurz TSP) genannt. Dadurch wurde das Zusammenwirken zwischen Chassis und Gehäuse berechenbar.
Der komplette Satz Thiele & Small Parameter besteht aus:
der mechanischen Abteilung
- Bewegte Masse (inkl. Luftlast) Mms (Mass mechanic speaker)
- Mechanische Nachgiebigkeit der Aufhängung Cms (Compliance mechanic speaker)
- Freiluft Resonanzfrequenz Fs (Frequency speaker)
- Abstrahlende Oberfläche (Membranfläche) Sd (Surface diagraphm)
- Äquivalentes Luftvolumen Vas (Volume acoustic speaker)
- Mechanischer Wiederstand Rms (Resistance mechanic speaker)
- Mechanische Güte (Freiluft) Qms (Q (=Güte) mechanic system)
der elektrischen Abteilung
- Gleichstromwiderstand der Schwingspule Rdc (Resistance direct current)
- Induktivität der Schwingspule Lvc (Induction voice coil)
- Kraftfaktor BL (= Magnetfeldstärke · Drahtlänge im Luftspalt)
- Elektrische Güte (Freiluft) Qes (Q electrical system)
Nicht alle Werte werden von den Herstellern zur Verfügung gestellt und zur groben Abschätzung reichen auch die 3 wichtigsten aus:
- Normalerweise strahlen dynamische Lautsprecher erst oberhalb ihrer Resonanzfrequenz (Fs) nennenswert Schall ab. Hier trennt sich der Basslautsprecher (Fs < 50 Hz) von Mitteltöner (Fs > 100 Hz), auch wenn sie von außen gleich aussehen.
- Wenn ich den Lautsprecher in ein Gehäuse einbauen will, dann wird das sog. Äquivalentvolumen (Vas), ganz wichtig. Dieser Wert ist nicht so ganz einfach zu verstehen. Wir hatten oben schon gesehen, dass beim Drücken auf die Membran die Einspannung eine Gegenkraft aufbringt (z.B. 1 N für 1 mm Hub). Wenn man einen Lautsprecher in ein geschlossenes Gehäuse einbaut dann bewirkt das eingeschlossene Luftpolster, dass für dieselbe Auslenkung wie uneingebaut eine höhere Kraft aufgewendet werden muss. Wenn ich den Lautsprecher nun in ein Gehäuse mit dem Volumen Vas einbaue, dann muss gerade die doppelte Kraft aufgewendet werden - die "Luftfeder" ist genau so steif wie die mechanische Aufhängung. Vas ist demnach von der mechanischen Nachgiebigkeit Cms und der Membranfläche Sd abhängig.
- Die 3. Größe im Bunde ist die Gesamtgüte Qts. Sie setzt sich zusammen aus der mechanischen Güte Qms und der elektrischen Güte Qes. Es gilt:
Qts = (Qms · Qes) / (Qms + Qes)
Während der mechanische Teil des Lautsprechers bei jeder Anregung am liebsten "stundenlang" mit seiner Resonanzfrequenz ausschwingen möchte versucht der elektrische Teil dem mechanischen Teil unabhängig davon seinen Willen aufzuzwingen und genau dem Eingangssignal zu folgen. Je länger der mechanische Teil ausschwingen würde, desto geringere mechanische Verluste Rms weist das System auf und desto höher ist die mechanische Güte Qms. Je besser Spule und Magnet den Lautsprecher bei der Resonanzfrequenz trotzdem im Griff haben, desto höher ist der Kraftfaktor und desto niedriger ist Qes.
So, das waren die Top 3 der TSP. Hier noch ein paar Erläuterungen zu den anderen Größen:
- Da sich die Sicke nicht komplett wie die Membran bewegt, wird bei der Berechnung der effektiven Membranfläche Sd nur die Hälfte der Sicke mit zur Membran gerechnet. Die "Tiefe" der Membran spielt übrigens keine Rolle, da nur die effektive Membranfläche in Bewegungsrichtung zählt.

- Der Kraftfaktor BL ist der Indikator für die Antriebskraft des Chassis. Wenn man auf die Membran eines liegenden Chassis eine unmagnetische Zusatzmasse legt und durch die Schwingspule einen Strom schickt bis die Membran wieder in ihre Ursprungslage zurückgekehrt ist, so ist: BL = Zusatzmasse [kg] · 9.81 [m/s²] / Strom [A]
- Eine (Schwing-) Spule hat durch die Länge des verwendeten Drahtes nicht nur einen Gleichstromwiderstand Rdc sondern auch eine Induktivität Lvc (weitere Infos zu diesen Begriffen in den Grundlagenartikeln Frequenzweichen. Da die Schwingspule nicht in Ruhe auf dem Schreibtisch liegt sondern sich noch in einem Magnetfeld bewegt tritt der Effekt der Gegeninduktion auf. Daher ist der Wert für Lvc nicht so ohne weiteres aus der Impedanzmessung abzulesen.
Das sollte für den Anfänger reichen. Wie die genauen technischen Zusammenhänge sind und wie man bei der Messung der Parameter berücksichtigen muss wird zu einem späteren Zeitpunkt im Artikel "TSP-Messen für Fortgeschrittene" erklärt.
Es folgt noch die Bildschirmkopie des Programms TSP-Check, mit dem man die Konsistenz der Thiele & Small Parameter testen kann. Interessanterweise hängen nämlich alle TSPs voneinander ab, wie man in der rechten Spalte des Bildes sehen kann. Mit dem Programm findet man sehr schnell fehlende Größen, Ungereimtheiten in Datenblättern und "Mondangaben" heraus. Gerade bei den Wirkungsgradangaben wird gerne etwas "gemogelt".

Kommentare
ich habe eine subwoofer der marke raveland flash bass 88 8 ohms 350 watt 20 cm durchmesser und einen subwopfer der marke raveland flash bass 128 500 watt 8 ohms 30 cm durchmesser
ich suche dafür den passenden Volumengehalt!
köönt ihr mir da weitrthelfen????
Detailliert beschrieben im "Basskochbuch" des Sonderheftes "Lautsprecherbau" von Elektor.
allenfalls..... dank der kompetenz des autors hier auch komplexere mechanische, physikalische... auch elektrische- bzw. elektrotechnische zusammenhänge, gemein verständliche analogien zur hilfe nehmend, darzustrellen..... sollte dieser artikel in jeder verdammten "klang und ton" oder "hifi hobby" etc zu anfang und am ende der zeitschrift, und zwar in jeder ausgabe gedruckt werden. verstehen ist mit- und unter nicht schlimm.
danke auch im namen meiner crew (christopb Brüx -- dolphin-sound-studios hamburg)