Feinheiten bei Filtern 2. Ordung
In den ersten beiden Teilen der Artikelserie zum Thema Frequenzweichen ging es um einfache Verbiegeschaltungen, Impedanzentzerrung und Pegelanpassung.
Im 3. Teil sollen spezielle Aspekte bei Filtern 2. Ordnung behandelt werden. Wir starten zunächst wieder mit unserem idealen Chassis aus dem 1. Teil (konstanter Frequenzgang von 90 dB und Impedanz von 8 Ohm). Alle Schaltungen sind - wie gewohnt - auch als Boxsim-Projekte in einer gemeinsamen ZIP-Datei (67 kB) downloadbar. Im Menüpunkt "Extras / Auslegung Standardweichen" ergeben sich für einen Hochpass 2. Ordnung mit einer Trennfrequenz von 1000 Hz die Werte 1.801 mH und 14.07 µF:
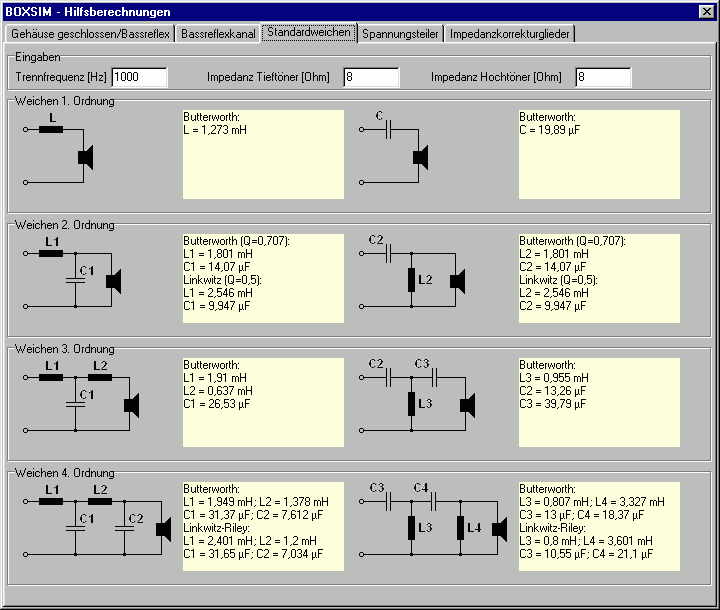
Diese Werte runden wir in gewohnter Manier erst mal auf den nächsten Wert der E12-Reihe.
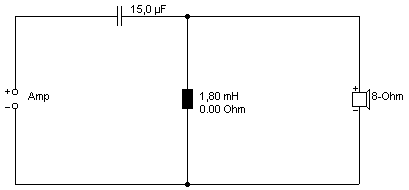
Neben dem "idealen" Spulenwert von 1.8 mH (schwarze Kurve) gucken wir mal was passiert, wenn man die Spule jeweils um 2 Stufen der E12-Reihe erniedrigt (orange, rot) bzw. erhöht (grün, blau):
Name des Boxsim-Projekts: 8_Ohm_HP2.bpj
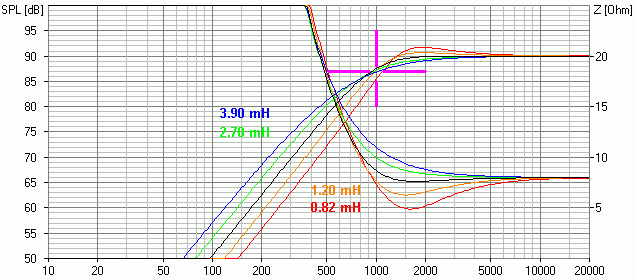
-> die Trennfrequenz bleibt weitgehend konstant!
-> der Pegel ändert sich vor allem um die Trennfrequenz herum (kleinere Spule -> steiler mit "Überschwingen")
-> die Impedanz im Bereich der Trennfrequenz ändert sich (kleinere Spule -> niedrigere Impedanz)
Und was passiert, wenn der Widerstand der Spule sich verändert?
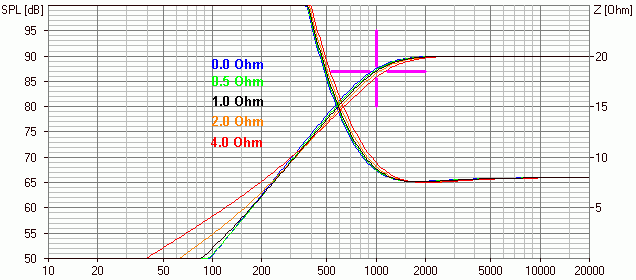
-> das tut sich kaum etwas -> Feinjustage!
Bleibt nur die Frage: funktioniert das beim Tiefpass genau so? Hier kann man neben dem Gleichstromwiderstand der Spule auch noch einen Reihenwiderstand zum Kondensator als zusätzliche Stellschraube einfügen:

Und wieder halten wir das Serienelement konstant (in diesem Fall die Spule mit 1.8 mH und 0 Ohm) und variieren nur den Kondensator um jeweils 2 Stufen der E12-Reihe:
Name des Boxsim-Projekts: 8_Ohm_TP2.bpj
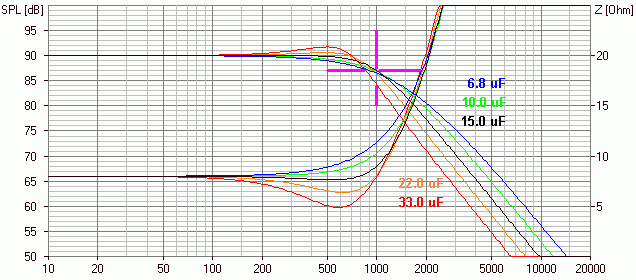
-> die Trennfrequenz bleibt weitgehend konstant!
-> der Pegel ändert sich vor allem um die Trennfrequenz herum (größerer Kondensator -> steiler mit "Überschwingen")
-> die Impedanz im Bereich der Trennfrequenz ändert sich (größerer Kondensator -> niedrigere Impedanz)
Im obigen Beispiel war der Reihenwiderstand zum Kondensator 0 Ohm. Und was passiert wenn man diesen Widerstand verändert?
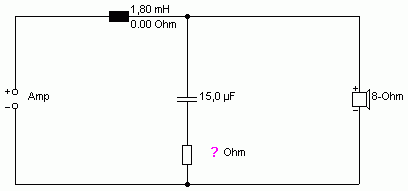
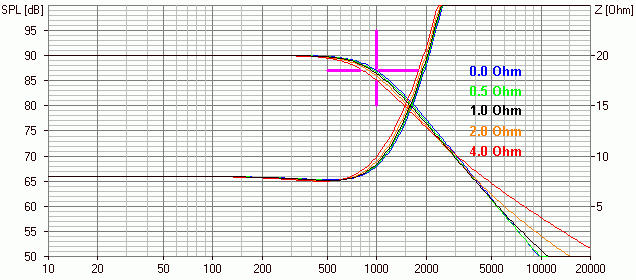
-> das tut sich kaum etwas -> Feinjustage!
Also im Großen und Ganzen ist das genau so wie beim Hochpass - halt nur anders herum. Beim Tiefpass kommt jedoch noch hinzu, dass die Serienspule immer einen Innenwiderstand hat. Wenn man den von 0 bis 4 Ohm variiert ergibt sich folgendes Bild (der Serienwiderstand zum Kondensator ist hier immer 0 Ohm):
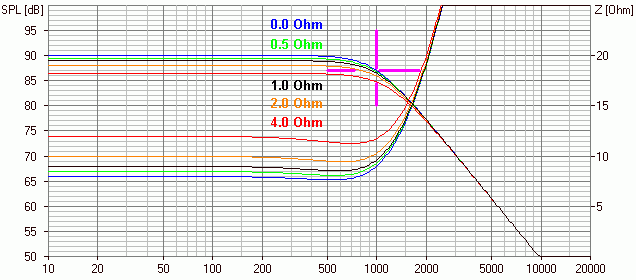
-> der Innenwiderstand reduziert den Pegel im Durchlassbereich -> das kann gewollt sein!
-> bei höherem Innenwiderstand steigt die Trennfrequenz (= 3 dB Abfall) zudem leicht an
Praktisches Beispiel:
Zum Abschluss wenden wir das Gelernte mal an zwei praktischen Beispielen an. Dazu erzeugen wir zunächst ein Boxsim-Projekt mit einen VISATON AL130M, den wir in ein 5 Liter großes, geschlossenes Gehäuse einbauen. Die Größe der Schallwand ist 32 x 90 cm und der AL130M ist 2 cm außermittig und 9 cm von oben angeordnet.
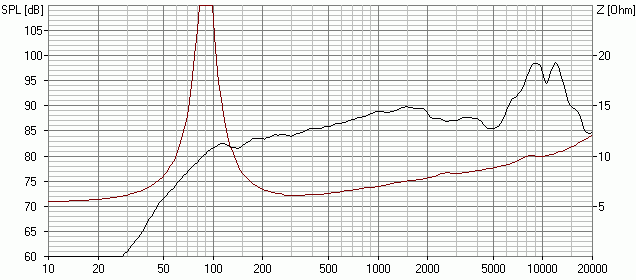
Damit ergibt sich der folgende Frequenzgang:
Name des Boxsim-Projekts: AL130M_Direkt.bpj
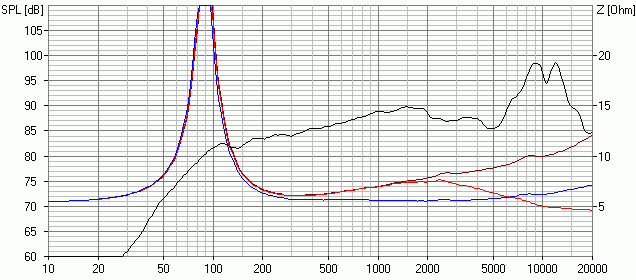
So, und da wollen wir jetzt mal bei 2 kHz mit 12 dB/Oktave die hohen Frequenzen wegfiltern. Zunächst könnte man ja mal eine Impedanzentzerrung für die Schwingspuleninduktivität zaubern, so als Fingerübung. "Leider" funktioniert die im 2. Teil beschriebene Vorgehensweise hier nicht auf Anhieb (es würde sich 5.6 Ohm und 3.3 µF ergeben -> rote Kurve). Mit etwas Rumprobieren kommt man schließlich auf 12 µF und 15 Ohm (blaue Kurve):
Name des Boxsim-Projekts: AL130M_TP2_2k.bpj
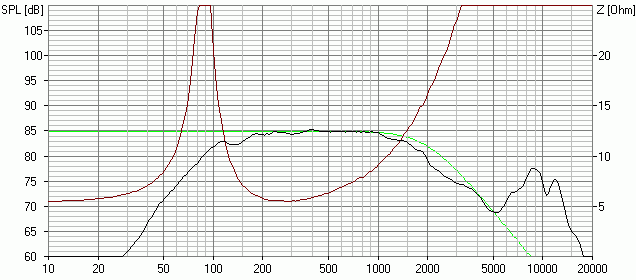
So, die Impedanz wäre nun recht flach, jetzt kann man die Formeln anwenden. Aber halt: der Frequenzgang des Chassis steigt ja kontinuierlich an, den Anstieg müssen wir erst mal mit einer Spule bremsen. Wenn wir das Niveau auf 85 dB "einfrieren" wollen benötigt man eine Spule von 1.2 mH - wie man durch Herumprobieren schnell herausfindet (grüne Kurve: idealer Tiefpass 2. Ordnung bei 2 kHz auf Niveau 85 dB) :
Name des Boxsim-Projekts: AL130M_TP2_2k.bpj
Dann ist der Pegel bei 2 kHz aber schon etwas zu tief -> da müsste man mit einem Kondensator noch etwas "nachhelfen" und würde gleich eine höhere Steilheit oberhalb von 2 kHz erreichen. Leider klappt das nicht so richtig. Entweder steigt auch der Wert unterhalb von 2 kHz wieder an oder die "Nachhilfe" bei 2 kHz reicht nicht aus. Hmh, was wäre denn ganz ohne Impedanzentzerrung? Die 1.2 mH Spule funktioniert immer noch, und mit einem 3.3 µF Kondensator kann man noch etwas nachhelfen:
Name des Boxsim-Projekts: AL130M_TP2_2k.bpj
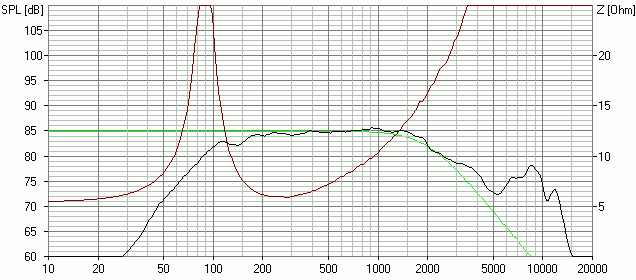
Jetzt stört nur noch die Resonanz bei 9 kHz. Da war doch was mit Saugkreisen parallel zum Lautsprecher? Kann man nicht einfach den 3.3 µF Kondensator mit einer richtig dimensionierten Spule kombinieren? Hier gibt es noch einmal den entsprechenden ONLINE-Rechner:
Mit einer Spule von 0.1 mH und einem Reihenwiderstand von 1.5 Ohm ergibt sich das folgende Verhalten:
Name des Boxsim-Projekts: AL130M_TP2_2k.bpj
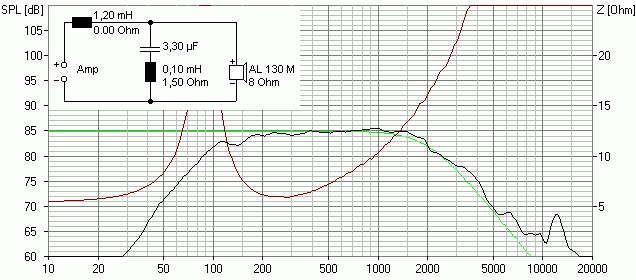
Das ist die Schaltung mit den wenigsten Bauteilen, die der Zielfunktion (grüne Kurve) am nächsten kommt. Obwohl es sich nominell um einen (viel zu tief einsetzenden) 6 dB Tiefpass mit Saugkreis handelt und die Filterfunktion fast nichts mit einer 12 dB-Weiche nach Lehrbuch zu tun hat ähnelt die akustisch wirksame Filterfunktion (bestehend aus Chassis + Weiche) verblüffend einem Tiefpass 2. Ordnung bei 2 kHz. Und darauf kommt es schließlich an!
Merke: Abweichungen von der Zielfunktion, die 20 dB unter dem Nennpegel liegen, können sich im ungünstigsten Fall um +/- 0.8 dB bemerkbar machen. Daher können sie in der Regel vernachlässigt werden.
Beim zweiten Beispiel handelt es sich um einen Hochpass. Auch hier erzeugen wir zunächst ein Boxsim-Projekt mit einen VISATON DSM50FFL, dessen Frequenzgang wir wie gemessen übernehmen (beim Eintrag "Messung der Frequenzgänge erfolgte" wählt man dazu einfach die Option "5. zu simulierende Box"). Das Gehäuse bringt der DSM50FFL schon mit, daher brauchen wir uns hier nichts zu überlegen. Den DSM50FFL haben wir genommen, da er ein ausgeprägtes Impedanzmaximum besitzt und daher nicht so einfach zu "bändigen" ist. So sieht der DSM50FFL aus, wenn man ihn direkt anschließt:
Name des Boxsim-Projekts: DSM50FFL_Direkt.bpj
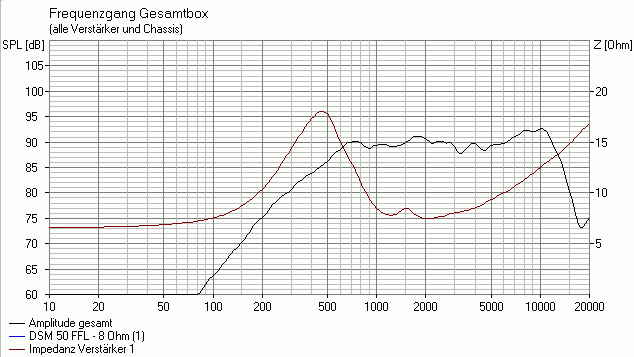
-> Wirkungsgrad ca. 90 dB/2.83/m
-> Impedanzmaximum von 18 Ohm bei ca. 450 Hz
-> konstante Impedanz von 8 Ohm zwischen 1 und 3 kHz
Als Faustformel sollte man bei einem Chassis mit ausgeprägtem Impedanzmaximum (kein Ferrofluid) frühestens eine Oktave oberhalb der Resonanzfrequenz trennen. Damit die 50mm Kalotte einigermaßen breitbandig eingesetzt werden kann peilen wir mal eine Trennfrequenz von 1 kHz an. Wenn man in "Extras / Auslegung Standardweichen" eine Trennfrequenz von 1000 Hz und eine Impdanz von 8 Ohm einträgt ergibt sich ein Kondensator von 14 µF (den wir auf den nächstgelegenen Wert der E12-Reihe von 15 µF aufrunden) und eine Spule von 1.8 mH. Diese Beschaltung ergibt folgendes Ergebnis (die grüne/blaue/magentafarbene Kurve ist der Verlauf eines idealen Hochpassfilters 2./3./4. Ordnung mit Butterworth-Charakteristik und einer Trennfrequenz von 1000 Hz):
Name des Boxsim-Projekts: DSM50FFL_HP2_1k.bpj
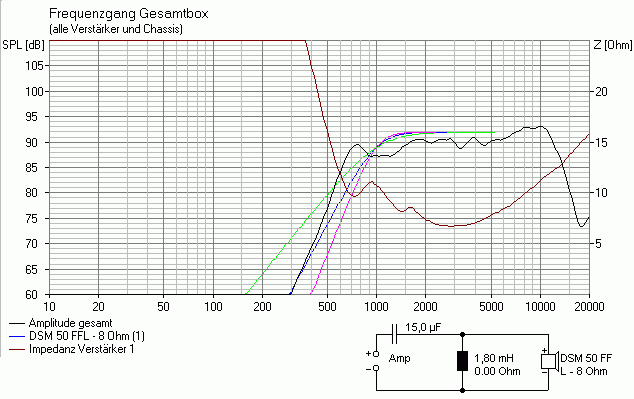
-> uups, das ging daneben! Schon ab 1500 Hz geht es bergab und bei 750 Hz ist ein starkes "Aufbäumen" zu erkennen
Es fällt auf, dass der Abfall unterhalb der Trennfrequenz viel steiler als die gewünschten 12 dB/Oktave sind (grüne Kurve). Der Verlauf ähnelt mehr einem Hochpassfilter 4. Ordnung (magentafarbene Kurve), allerdings nach "links" (= zu tieferen Frequenzen) verschoben. Das ist auch nicht weiter verwunderlich. Das Chassis selbst fällt ja unterhalb seiner Resonanzfrequenz "von alleine" mit 12 dB/Oktave ab (akustisch). Weitere 12 dB/Oktave kommen aus dem elektrischen Filter -> der akustische Gesamtverlauf entspricht einem Hochpassfilter 4. Ordnung mit einer Steilheit von 24 dB/Oktave!
Bei einem elektrischen Filter von 6 dB/Oktave ergäbe sich also ein Gesamtabfall von 18 dB/Oktave. Damit das Filter richtig funktioniert muss das Impedanzmaximum allerdings zuvor auf jeden Fall entzerrt werden (s. 2. Teil der Artikelserie). Sonst sieht das Ergebnis total daneben aus. Das wäre eine kleine "Fingerübung" für den interessierten Leser. Bei Boxsim-Projekt DSM50FFL_HP2_1k.bpj muss man eigentlich nur die Spule "entfernen" und den Wert des Kondensators richtig wählen - und nach dem Schreck die Impedanzlinearisierung einfügen . . .
Na gut, bleiben wir beim "elektrischen" Hochpassfilter 2. Ordnung: was muss ich denn machen, damit die Trennfrequenz nach oben rutscht? Nach ein paar Iterationen kommt man zu folgendem Ergebnis:
Name des Boxsim-Projekts: DSM50FFL_HP2_1k.bpj
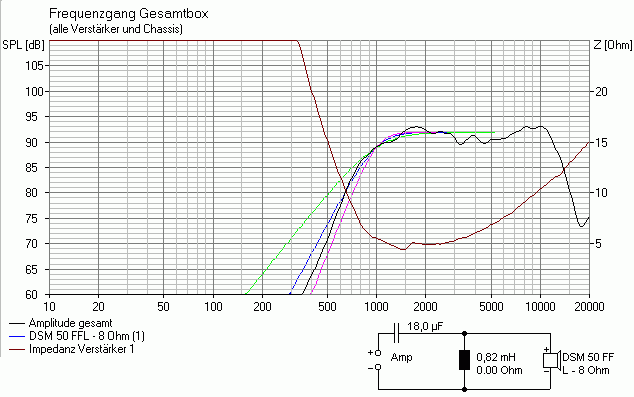
-> bis auf die kleine Überhöhung bei ca. 1700 Hz sieht das doch "unten rum" schon gut aus!!!
-> die Impedanz geht etwas in die Knie (4.5 statt 7.5 Ohm)
Das ist die Schaltung mit den wenigsten Bauteilen, die der Zielfunktion (magentafarbene Kurve) am nächsten kommt. Obwohl es sich nominell um einen 12 dB Hochpass (mit viel zu kleiner Spule) handelt ähnelt die akustisch wirksame Filterfunktion (bestehend aus Chassis + Weiche) verblüffend einem Hochpass 4. Ordnung bei 1 kHz. Und darauf kommt es schließlich an!
Im 4. Teil der Artikelserie geht es um Feinheiten bei Filtern 3. Ordnung. Unter anderem wird die Philosophie hinter dem von KEF in den 80er Jahren eingeführten Schlagwort "Acoustical Butterworth Filter" erläutert und es werden Dimensionierungshinweise gegeben.