Besonderheiten bei Bandpässen
In den ersten 4 Teilen der Artikelserie zum Thema Frequenzweichen ging es um einfache Verbiegeschaltungen, Impedanzentzerrung/Pegelanpassung und Feinheiten bei Filtern 2. und 3. Ordnung. Bisher wurden nur einfache Hoch- ODER Tiefpassfilter behandelt, wie sie z.B. für 2-Wege-Lautsprecher benötigt werden.
Bei einer 3-Wege-Box muss der Mitteltöner jedoch sowohl vor tiefen Tönen bewahrt (= Hochpass) als auch von hohen Tönen befreit (= Tiefpass) werden. Somit kommen beide Filtertypen gleichzeitg zum Einsatz und lassen somit nur ein Frequenzband durch - deswegen heißen diese Filter auch Bandpassfilter. Solange die beiden Trennfrequenzen weit genug auseinander liegen kommen sich die beiden Filter nicht ins Gehege und können weitestgehend isoliert betrachtet werden.
Im 5. Teil soll es aber genau um diese kritischen Fälle gehen. Wir starten zunächst wieder mit unserem idealen Chassis aus dem 1. Teil (konstanter Frequenzgang von 90 dB und Impedanz von 8 Ohm). Alle Schaltungen sind - wie gewohnt - auch als Boxsim-Projekte in einer gemeinsamen ZIP-Datei (24 kB) downloadbar.
Ideale Bandpässe mit Filtern 1. Ordnung
Berechnen wir zunächst eine 3-Wege-Box mit 6 dB-Filtern bei relativ weit auseinander liegenden Trennfrequenzen von 200 und 2000 Hz. Im Menüpunkt "Extras / Auslegung Standardweichen" ergeben sich die Werte 6.366 mH (Bass), 99.48 µF und 0.6366 mH (MT) und 9.948 µF (HT):
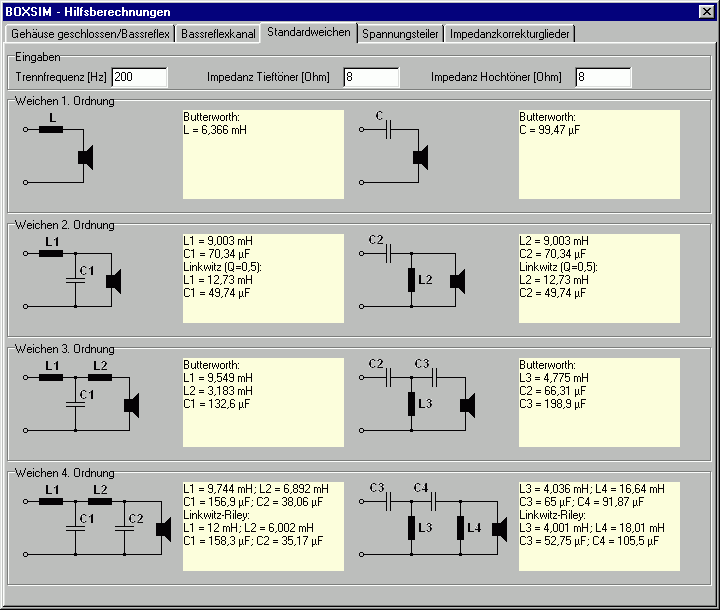
Diesmal runden wir die Werte ausnahmsweise mal nicht:
Name des Boxsim-Projekts: 8_Ohm_3W1_200_2k.bpj

-> Uups, was ist denn da passiert? Rechnet Boxsim nicht richtig?
Hmmhh, das sollte doch eigentlich eine ganz flache Kurve ergeben, oder? Na ja, eigentlich sieht man in der Literatur immer nur die Überlagerung bei 2-Wege-Weichen. Also, lassen wir doch mal den Hochtöner weg und den Mitteltöner nach oben durchlaufen:
Name des Boxsim-Projekts: 8_Ohm_3W1_200_2k.bpj

-> Aaahh, so sollte es aussehen. Na bitte, klappt doch!
So, und jetzt dasselbe mit nach oben begrenztem Mitteltöner:
Name des Boxsim-Projekts: 8_Ohm_3W1_200_2k.bpj

-> Arghh, da haben wir den Salat . . .
Die beiden Weichenbauteile des Mitteltöners beeinflussen sich offenbar gegenseitig und führen zu einer Überhöhung des Mitteltöners. OK, spendieren wir dem Mitteltöner einfach einen Vorwiderstand um das zu kompensieren:
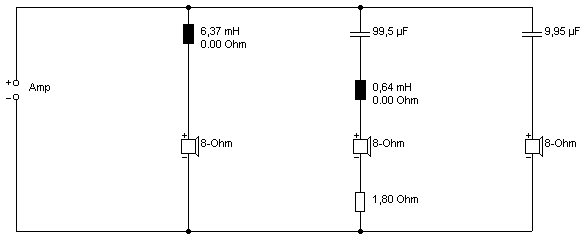
Name des Boxsim-Projekts: 8_Ohm_3W1_200_2k.bpj

-> Mit 1.8 Ohm sieht es fast perfekt aus . . .
Eieiei, wer hätte das gedacht. Und dabei liegen die Trennfrequenzen noch sehr weit auseinander (10:1). Wenn man die Übernahmefrequenz zwischen Bass und Mitteltöner auf 400 Hz anhebt (6.366 -> 3.183 mH, 99.48 -> 49.74 µF) sieht es wie folgt aus:

-> Uups, das wird ja noch schlimmer!
Die Überhöhung beträgt jetzt schon 2.6 dB und die -3 dB Frequenzen des Mitteltöners liegen bei 350 und 2250 Hz! Jetzt müsste man schon einen Widerstand von 3.9 Ohm einführen um die Überhöhung zu kompensieren. Genau genommen müssten auch die Werte des Mitteltöners angepasst werden (Kondensator kleiner und Spule größer). Gar nicht so einfach . . .
Übrigens: die Reihenfolge der Bauteile beim Mitteltöner ist egal! Da alle Bauteile in Reihe liegen fließt derselbe Strom durch alle Bauteile . . .
Ideale Bandpässe mit Filtern 2. Ordnung
Und wie sieht das bei Filtern 2. Ordnung aus. Wir fangen wieder mit relativ weit auseinander liegenden Trennfrequenzen von 200 und 2000 Hz an. Im Menüpunkt "Extras / Auslegung Standardweichen" ergeben sich die folgenden Werte:
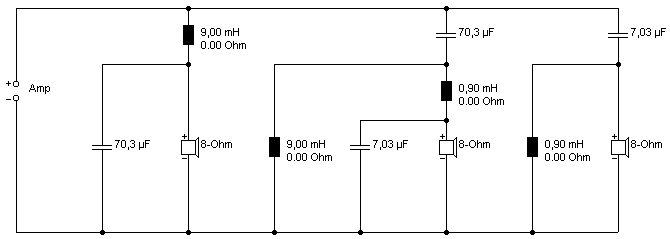
Und wieder lassen wir zunächst den Hochtöner weg und den Mitteltöner durchlaufen:
Name des Boxsim-Projekts: 8_Ohm_3W2S_200_2k.bpj
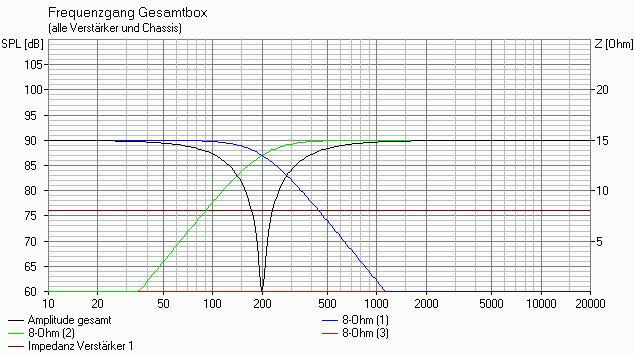
-> Uups, da war doch was mit Verpolen . . .
| Kleine Weichenkunde: |
Hier der dort beinhaltete ONLINE-Rechner: |
Bei Filtern 2. Ordnung beträgt die Phasendrehung bei der Übernahmefrequenz (- 3 dB) also + bzw. - 90°. Somit ist die relative Phase 180° und die beiden Anteile löschen sich aus. Dies kann man durch Verpolen eines Chassis beheben:
Name des Boxsim-Projekts: 8_Ohm_3W2S_200_2k.bpj

-> Hmmhh, da war doch was mit einer Überlagerung bei - 6 dB . . .
Jetzt haben beide Anteile von Bass und Mittelton bei der Trennfrequenz die Amplitude - 3 dB und eine relative Phase von 0° -> sie überlagern sich perfekt und führen zu einem Summenpegel von + 3 dB (s. o.). Aahh ja, daher kommt ja auch der Wunsch, dass sich die Chassis beim - 6 dB-Punkt treffen und dort dieselbe Phase haben sollen . . .
Ja, und woher bekomme ich jetzt die benötigten Werte? Leider berechnen alle uns bekannten Weichenrechner die - 3 dB-Trennfrequenz - außer natürlich unser eigener! Wenn man die dort berechneten Werte einsetzt treffen sich die Chassis tatsächlich beim - 6 dB-Punkt:
Name des Boxsim-Projekts: 8_Ohm_3W2S_200_2k-6.bpj

-> Bei der Trennfrequenz kommt es jetzt ganz gut hin, aber was ist denn da oben rum los . . .
Der -6 dB-Punkt liegt am oberen Ende nicht bei 2000 Hz und es ergibt sich eine Überhöhung des Mitteltöners. Wenn man den Hochtöner auch noch zuschaltet sieht es so aus:

Name des Boxsim-Projekts: 8_Ohm_3W2S_200_2k.bpj

-> Irgendwie unsymmetrisch, oder . . .
Wieder scheinen sich die Weichenteile irgendwie gegenseitig zu beeinflussen (ACHTUNG: die minimale Impedanz sinkt auf nur noch 5.7 Ohm ab!!!). Im obigen Fall wurden beide Filter hintereinander geschaltet: zuerst der Hochpass, dann der Tiefpass. Wenn man beide Filter ineinander verschachtelt gibt es einen Reihenschwingkreis und einen Parallelschwingkreis:

Name des Boxsim-Projekts: 8_Ohm_3W2P_200_2k.bpj
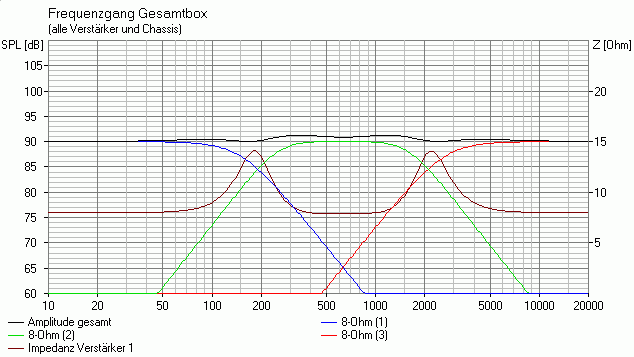
-> Schon besser (Zmin = 8 Ohm), aber der Mitteltöner braucht noch einen "Dämpfer" . . .
Mit einem Vorwiderstand von 1.5 Ohm sieht es so aus:
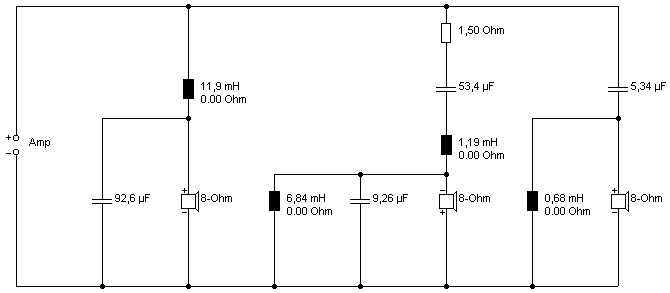
Name des Boxsim-Projekts: 8_Ohm_3W2P_200_2k.bpj

-> Na also!
Und was ist wenn wir die untere Trennfrequenz wieder auf 400 Hz anheben?
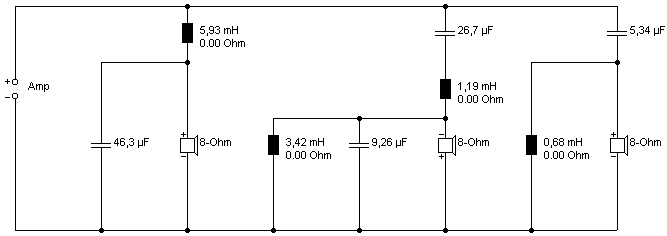
Name des Boxsim-Projekts: 8_Ohm_3W2P_400_2k.bpj

-> Die Überhöhung beim Mitteltöner ist noch etwas gestiegen und beträgt nun fast 2 dB . . .
Halten wir für ideale Bandpässe 2. Ordnung fest:
- Benachbarte Chassis müssen verpolt werden
- Dann muss bei der Trennfrequenz der Abfall 6 dB betragen
- Die Reihenschaltung der Teilfilter führt zu einem unsymmetrischen Verhalten und evtl. einem kritischen Impedanzminimum
- Die Verschachtelung der Teilfilter führt zu einem symmetrischen Verhalten mit unkritischem Impedanzverlauf
- Die Lautstärke des Mitteltöners steigt auf jeden Fall an (je schmaler der Bandpass desto mehr)
Ideale Bandpässe mit Filtern 3. Ordnung
Auf dieselbe Art und Weise versuchen wir die Bandpässe 3. Ordnung zu verstehen. Wir fangen wieder mit relativ weit auseinander liegenden Trennfrequenzen von 200 und 2000 Hz an. Im Menüpunkt "Extras / Auslegung Standardweichen" ergeben sich die folgenden Werte:

Vielleicht ein paar Worte zur Darstellung der Weiche:
- Die Chassis sind von links (Bass) nach rechts (Hochtöner) angeordnet
- Die Weichen laufen von "oben" nach "unten"
Diese Darstellung ist platzsparender als die übliche Darstellung (Chassis von oben nach unten, Weichen von links nach rechts) weil die freien Drahtbrücken entfallen.
Und wieder lassen wir zunächst den Hochtöner weg und den Mitteltöner durchlaufen:
Name des Boxsim-Projekts: 8_Ohm_3W3S_200_2k.bpj

-> Perfekt! Und das ohne Verpolen und "trotz" Überlagerung beim -3 dB-Punkt . . .
Merke: bei allen "ungeraden" Filterordnungen müssen die Chassis idealerweise nicht verpolt werden und sich beim -3 dB-Punkt treffen!
Na, dann wollen wir mal sehen was passiert, wenn wir den Mitteltöner nach oben hin filtern:
Name des Boxsim-Projekts: 8_Ohm_3W3S_200_2k.bpj

-> Leichter Einbruch beim Übergang Bass und MT
-> Leichte Überhöhung des MT am oberen Ende verbunden mit einem Absinken der Impedanz
-> Das kennen wir doch schon vom Bandpass 2. Ordnung !
Wenn man nun noch den Hochtöner dazu packt sieht es so aus:
Name des Boxsim-Projekts: 8_Ohm_3W3S_200_2k.bpj

-> der Amplitudenverlauf ist zwar nicht mehr perfekt aber noch akzeptabel
-> Das Absinken der Impedanz am oberen Ende des MT ist allerdings unschön
Vielleicht hilft ja wieder die Verschachtelung des Bandpasses beim Mitteltöner. Nur: wie sieht das denn bei einem 18 dB-Filter aus?
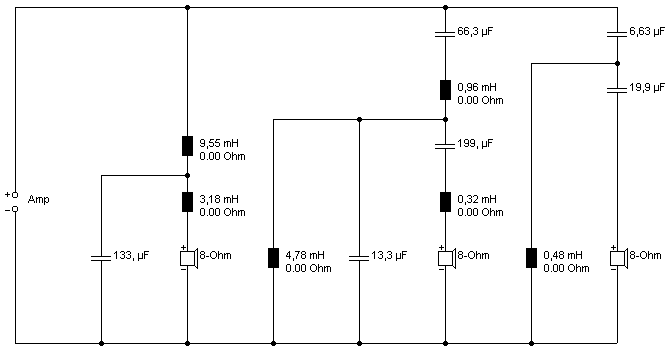
Name des Boxsim-Projekts: 8_Ohm_3W3P_200_2k.bpj

-> fast perfekt!
Die -3 dB-Punkte des Bandpasses rutschen etwas nach außen und sorgen so für das geringfügige Absinken der Impedanz im Bereich des Überganges und den leichten Pegelverlust beim Mitteltöner. Was passiert eigentlich, wenn man die Chassis verpolt? Bei "ungeraden" Filterordnungen würde sich idealerweise mit beiden Polungsvarianten dieselbe Überlagerung ergeben:
Name des Boxsim-Projekts: 8_Ohm_3W3P_200_2k.bpj

-> jetzt gibt es eine kleine Überhöhung im Frequenzgang!
Wenn man die Trennfrequenz des Bandpasses um 10% nach oben und unten verschiebt sollten die -3 dB-Punkte "richtig" liegen:

Name des Boxsim-Projekts: 8_Ohm_3W3P_200_2k_Mod.bpj

-> voila!
So, zum Abschluss erhöhen wir wieder die untere Trennfrequenz auf 400 Hz (nur verschachtelte Anordnung, ohne Fummelfaktor 10%):

Name des Boxsim-Projekts: 8_Ohm_3W3P_400_2k.bpj

-> Hmmhh, der Bandpass "verbreitert" sich noch etwas stärker und deformiert den Gesamtfrequenzgang deutlich
Da hilft leider auch keine Fummeln. Die verschaltete Beschaltung bewirkt, dass der "Knick" vom Durchlass- in den Sperrbereich "eckiger" ist. Zwischen den beiden Eckfrequenzen des Bandpasses überlagert sich der Anteil des Mitteltöners sowohl mit dem Bass als auch dem Hochtöner. Der Pegel ist bei 900 Hz zwar schon auf -21 dB abgesunken, aber die Phasenlage hat noch nicht ihr Maximum von 270° erreicht sondern liegt zwischen 135 und 270°:

Laut Boxsim beträgt sie bei 900 Hz +/- 215° (der "Sprung" bei +/- 180° ist nur durch die Darstellung bedingt). Setzt man 0 und -21 dB sowie 215° in den ONLINE-Rechner weiter oben ein ergibt sich ein Summenpegel von -0.65 dB/-3.2°. Zieht man von diesem Wert erneut -21 dB/-215° ab ergibt sich -1.37 dB/-3.2° - voilà.
Merke: Auch Kleinvieh (= Pegel < -15 dB) macht Mist (= beeinflusst den Gesamtpegel)
Und warum hat das vorher als 2-Wege-System (Trennfrequenz 200 Hz) perfekt geklappt? Da hat sich die Phase des Mittel-/Hochtöners langsamer gedreht und erst später die 0° Marke erreicht. Dadurch war die relative Phase "günstiger" (konstant 90° Phasendifferenz).

Aktiv vs. Passiv
Wenn man sich das nichtideale Verhalten von passiven Mehrwegeweichen selbst mit idealen Chassis (konstante Impedanz, linearer Frequenzgang) so anguckt könnte einem der Gedanke kommen: "dann doch lieber aktiv!" Aber die Frage aller Fragen lautet: "funktioniert das besser"? Dazu haben wir die "kritischeren" 3-Wege-Systeme mit den Trennfrequenzen 400 und 2000 Hz einmal aktiv aufgebaut - natürlich nur virtuell.
Dazu muss man im Dialog "Datei/Projekteigenschaften" zunächst einmal die Anzahl der Verstärker auf 3 erhöhen:

Dann gibt es in der Menüleiste 2 neue Menüpunkte, nämlich "Verstärker 2" und "Verstärker 3". Jetzt muss man jeden Verstärker mit einer eigenen Weiche beschalten, was im Falle einer Aktivweiche denkbar einfach ist:

Die eigentliche Filterung wird nun im Dialog "Verstärker ?/Aktive Filter..." vorgenommen:

-> Bandpass 1. Ordnung bei 400 und 2000 Hz
Die Einstellungen für die Filterordnungen 1, 2 und 3 mit Butterworth-Charakteristik lauten wie folgt:
| Filter | Tiefpass 6 dB | Tiefpass 12 dB |
| 1. Ordnung (-3 dB) | F = F3 | |
| 2. Ordnung (-3 dB) | F = F3, Q = 0.707 | |
| 2. Ordnung (-6 dB) | F = 0.76*F3, Q = 0.707 | |
| 3. Ordnung (-3 dB) | F = F3 | F = F3, Q = 1 |
So sähe dann z.B. der Bandpass 3. Ordnung aus:

-> Bandpass 3. Ordnung bei 400 und 2000 Hz
Damit ergeben sich dann die folgenden Frequenzgänge für aktive 3-Wege-Kombinationen:
Name des Boxsim-Projekts: 8_Ohm_3W1A_400_2k.bpj

-> die Überhöhung beträgt aktiv "nur" 1.5 dB gegenüber 2.5 dB bei der passiven Weiche
Name des Boxsim-Projekts: 8_Ohm_3W2A_400_2k.bpj (Überlagerung bei -6 dB, MT verpolt)

-> die Überhöhung beträgt aktiv "nur" knapp 1 dB gegenüber 2 dB bei der passiven Weiche
-> bei der Aktivweiche stimmen allerdings noch die Trennfrequenzen des Bandpasses
Name des Boxsim-Projekts: 8_Ohm_3W3A_400_2k.bpj

-> die Überhöhung ist passiv und aktiv etwa gleich
-> bei der Aktivweiche stimmen allerdings noch die Trennfrequenzen des Bandpasses
Bei aktiven Filtern beeinflussen sich zwar die Trennfrequenzen nicht gegenseitig wie bei passiven Weichen, die Summenfunktion aller 3 Wege ist allerdings auch nicht perfekt. Die Abweichungen sind allerdings geringer als bei passiven Weichen und lassen sich auch von realen Impedanzen nicht beirren.
Reale Bandpässe
So, das Schema dürfte jetzt klar geworden sein, so dass sich eine Behandlung von Bandpässen 4. Ordnung erübrigen dürfte. Diese haben in der Praxis ohnehin nur eine geringe Bedeutung - zumindest bei passiven Weichen und auf der elektrischen Seite.
Bisher haben wir nur ideale Bandpassfilter betrachtet. Zum einen hatten alle Spulen einen Innenwiderstand von 0 Ohm, zum anderen waren alle Chassis identisch (Impedanz, Frequenzgang) und waren sogar an derselben Stelle auf der Schallwand montiert (Abmessungen und Chassisposition gemäß IEC-Schallwand):
Wenn man eine reale 3-Wege-Box aufbaut, dann sind die Chassis z.B. auf unterschiedlicher Höhe montiert. Außerdem haben sie üblicherweise unterschiedliche SchallEntstehungsOrte (SEO = unterschiedliche Tiefe). Dadurch werden zusätzliche "Freiheitsgrade" in das Design eingeführt, was die Sache nicht unbedingt leichter macht - selbst wenn man ideale Chassis hat. Bei großen Hör- bzw. Messentfernungen ist der Einfluss der unterschiedlichen Einbauhöhe weitgehend zu vernachlässigen - sofern man die Chassis nahe beieinander montiert. Schlimmer sieht es da schon mit dem Tiefenversatz durch den SEO aus. Beide Einflussfaktoren wirken in der Regel unterschiedlich auf den Frequenzgang (0°) und den Energiefrequenzgang (energetisches Mittel aller Abstrahlwinkel). Im folgenden Beispiel wurde nur der SEO (Menüpunkt "Chassis & Einbau / Chassis X", Reiter "Chassisdaten") auf 40 / 20 / 0 mm für Bass / MT / HT geändert (Basis: 0 / 0 / 0 mm als Referenz im Hintergrund):

-> Der Übergang MT / HT überlagert sich konstruktiver -> Überhöhung
Als Gegenmaßnahme müsste man nun die Trennfrequenzen so "auseinander ziehen", dass sich beide Chassis bei -6 dB überlagern. Da ist es dann vorbei mit der schönen Theorie.
In der Praxis versucht man bei allen Filterarten bei der Trennfrequenz eine möglichst konstruktive Überlagerung (= möglichst geringe relative Phase) zu erreichen. Das garantiert, dass man bei verschiedenen Mess- bzw. Ohrhöhen nicht "aus Versehen" eine noch effektivere Überlagerung bekommt - sprich einen fetten Querschläger. Da man den SEO bzw. die "Tiefe" eines Chassis in der Regel nicht mehr verändern kann (Ausnahme: verschiebbare Teilgehäuse) bleibt nur das "Spielen" mit den Trennfrequenzen und mehr oder weniger steilen Übergängen. Zusammen mit der Kompensation der Chassisfehler und dem Einfluss der Gehäusegröße bleibt ein breites Spielfeld zur Optimierung des Gesamtsystems. Boxsim sei Dank muss man nicht alles real aufbauen und durchmessen . . .
Im 6. Teil der Artikelserie geht es um das Thema Zielfunktion. Boxsim gibt neben dem Frequenzgang auf Achse auch den Energiefrequenzgang, den Frequenzgang bei bestimmten Winkeln, die Bündelung etc. an. Was bedeuten diese Angaben und welches dieser Ergebnisse sollte wie verlaufen damit es je nach Aufstellung und Raumakustik gut klingt?