Wer schon einmal mit einem Lautsprecher-Simulationsprogramm (z.B. Lasip, BoxSim, LspCAD etc.) gearbeitet hat musste sich mit dem Thema des "akustischen Zentrums" herumschlagen. Darunter versteht man den "scheinbaren" Schallentstehungsort eines Lautsprechers.
Leider ist dieser Ort nicht mit einem weißen Punkt auf der Membran gekennzeichnet. Es gibt zwar einige "Faustformeln" wie z.B. "Mittelpunkt der Schwingspule" oder "Beginn der (Staubschutz-) Kalotte", aber die Unzulänglichkeit dieser Orte und die Vielfalt der Faustformeln macht die Sache auch nicht gerade besser.
Die üblichen Messprogramme (z.B. HobbyBox, ATB etc.) geben zwar eine "akustische Phase" an, aber was wird da eigentlich angegeben? Die akustische Phase setzt sich aus 3 Teilen zusammen (wenn wir den rein elektrischen Teil und die Fehler des Mikrofons mal ausklammern):
- Mechanisch: Laufzeit von der Schwingspule zur Membranoberfläche
- Akustisch: Laufzeit von der Membranoberfläche zur Schallwandebene
- Akustisch: Laufzeit von der Schallwand zum Mikrofon
Laufzeit [s] = Umweg [m] / Schallgeschwindigkeit [m/s]
Bei 1 m sind das für Luft z.B. 1 / 343 = 0.00292 s = 2.92 ms. Je nach Frequenz hat ein Sinussignal dabei einen mehr oder weniger großen Teil seines 360°-Zyklus durchlaufen:
Phasenwinkel [°] = Frequenz [Hz] · Laufzeit [s] · 360°
Für 100 Hz sind das 105°, für 1000 Hz schon 1050° bzw. 2 komplette Zyklen + 330°. Man sieht, diese Werte werden sehr schnell "unhandlich" und hängen ja auch nur von der Entfernung des Mikrofons ab, sagen also nichts aus über die Eigenschaften des Lautsprechers an sich. Daher möchte man sich um diese "exzessive" Phase gar nicht kümmern und sie unter den Tisch fallen lassen. Das geht sehr schön, wenn man die Phase nicht misst sondern aus dem Schalldruckfrequenzgang per Hilbert-Transformation berechnet. Solange es sich um ein sog. Minimalphasensystem handelt darf man das auch ohne Weiteres machen. Leider geht damit auch die Lage des Schallentstehungsortes prinzipbedingt verloren, da ein Wegversatz eben nicht der Bedingung eines Minimalphasensystem gehorcht.
Die für das Chassis wesentliche Phaseninformation steckt im 1. und 2. Teil der obigen Liste. Diese dürfen bei einer absoluten Bestimmung der akustischen Phase nicht verloren gehen. Viele Programme messen daher die Impulsantwort (z.B. mit einem MLS-Signal oder 2-kanalig) und berechnen daraus den komplexen Frequenzgang mit Amplitude und Phase. Eigentlich müsste man als Startpunkt wieder den Beginn des Anregungssignals setzen und hätte dann wieder die lästige "exzessive" Phase mit dabei. Daher wird einfach so getan, als wäre die Anregung viel später erfolgt und zwar zu einem Zeitpunkt, den man mit einem Cursor manuell festlegen kann. Und da liegt der Hund begraben! Der Cursor müsste eigentlich in konstantem Abstand zur Anregung gesetzt werden. Stattdessen wird der Cursor aber in der Regel relativ zur Antwort gesetzt, wodurch es wieder keinen absoluten Bezug mehr gibt. Diese "absolute" akustische Phase brauche ich aber, sobald ich den Unterschied der akustischen Phase von zwei verschiedenen Chassis bestimmen will (wobei hier auch der Mikrofonabstand zu einer Bezugsebene konstant gehalten werden muss). Diese Differenz möchte ich der Einfachheit halb mal die "relative" akustische Phase nennen.
Eigentlich kann JustOct da gar nicht mitreden, denn es kennt nicht mal eine akustische Phase. Durch die Zusammenfassung aller Energie innerhalb eines 1/12 Oktavbandes geht nämlich per Definition die Phaseninformation verloren. Trotzdem kann man mit etwas List und Tücke die gewünschten Informationen ermitteln.
Die relative Phase
Bei einer reinen Simulation braucht man eigentlich die akustische Phase beider Chassis sowie deren Schallentstehungsorte. Dann kann man für eine beliebige Mikrofonposition (für die der angegebene Schalldruck-Frequenzgang und die akustische Phase allerdings noch gelten muss) die relative akustische Phase und damit die phasenrichtige Überlagerung beider Quellen im Übernahmebereich richtig berechnen.Wenn man aber schon ein Testgehäuse mit den in Frage kommenden Chassis aufgebaut hat, dann kann man an einer bestimmten Mikrofonposition aber auch die relative Phase berechnen, selbst wenn die Messungen - wie bei JustOct - gar keine Phaseninformation kennt. Wie soll das denn gehen?
Wenn man neben den Einzelchassis auch die Überlagerung beider Chassis misst, dann lässt sich daraus die relative Phase bestimmen. Denn mit den Pegeln der Einzelchassis kann sich der gemessene Summenpegel nur für eine bestimmte Phasendifferenz einstellen. Dazu müssen wir uns erst mal vergegenwärtigen, wie man denn gleichzeitig einen Schalldruckpegel und eine Phaseninformation darstellt. Dazu kann man "Zeiger" verwenden (Fachbegriff: Vektoren), deren Länge die Amplitude (in Pascal, nicht in dB) und deren Winkel (relativ zu einer Referenz) den Phasenwinkel wiedergibt. Die Addition von 2 Zeigern kann man sich am einfachsten graphisch vorstellen:
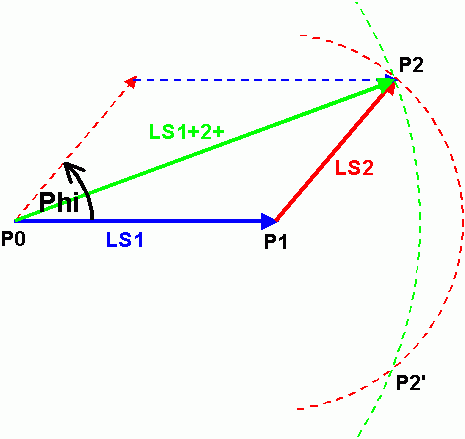
Durch die Messung der Schalldruckpegel ist die Länge der 3 Zeiger bekannt. Um den Winkel Phi zu ermitteln zeichnet man zuerst den Zeiger LS1 mit der Länge |LS1| in willkürlicher Richtung (z.B. 3 Uhr). An den Endpunkt des Zeigers LS1 muss man nun in unbekannter Richtung einen Zeiger der Länge |LS2| "kleben" um die Addition beider Zeiger zu vollführen. Der unbekannte Endpunkt des Zeiger LS2 liegt somit auf einem Kreis um den Punkt P1, dessen Radius |LS2| entspricht. Auf der anderen Seite wissen wir, dass die vektorielle Summe der Zeiger LS1 und LS2 die Länge |LS3| besitzt. Also muss der gesuchte Punkt auch gleichzeitig auf einem Kreis um P0 liegen, dessen Radius |LS1+2+| entspricht. Beide Kreise schneiden sich an 2 Punkten, wobei diese symmetrisch zum Zeiger LS1 liegen. Nun können die Zeiger LS2 und LS1+2+ eingezeichnet und der gesuchte Winkel Phi (bzw. Phi') bestimmt werden.
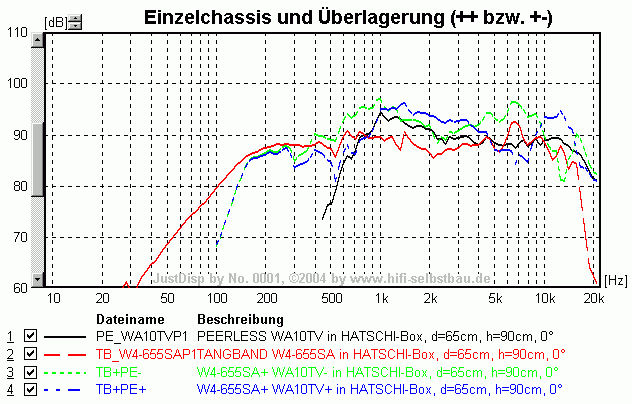
Sicherheitshalber sollte man eine 4. Messung machen, nämlich die Überlagerung beider Chassis bei Verpolung eines Chassis. Im Idealfall sollte sich derselbe Winkel Phi ergeben. Durch kleine Messfehler weichen die berechneten Winkel um < 2° voneinander ab, so dass der "wahre" Wert durch Mittelung beider Ergebnisse ermittelt wird.
Hinweis: Wenn der Pegelunterschied zwischen beiden Einzelchassis > 15 dB ist wird die Berechnung zunehmend ungenau! Glücklicherweise dominiert dann auch ein Chassis so sehr, dass die relative Phase auch nicht mehr von Belang ist . . .
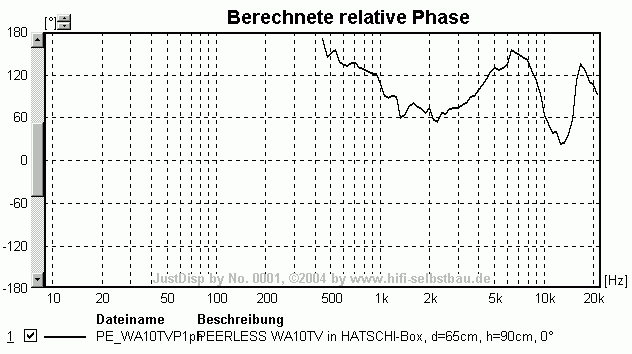
Der berechneten Phase sieht man zwar nicht mehr an, ob die Phasedifferenz durch Phasendrehung des LS1 oder LS2 oder einem etwaigen Tiefenversatz beider Chassis entstanden ist. Das ist aber auch uninteressant solange man an der Anordnung nichts mehr ändert!
"Mit welchem Recht nimmt man denn nun an, dass die Phase positiv ist und dass man sie dem Hochtöners zuschlagen muss?" könnte der aufmerksame, aber kritische Leser fragen. Diese Frage habe ich mir auch gestellt, und bin durch Studium unter anderem des Buches "Lautsprecherbau" von Vance Dickason (z.B. Seite 260) fündig geworden:
- bei einem Minimalphasensystem kann ich die akustische Phase aus dem Frequenzverlauf ermitteln. Bei flachem Frequenzgang - also im Übertragungsbereich - ist die akustische Phase 0°, bei ansteigendem Frequenzgang ist sie > 0°. Bei einem Anstieg von 6 bzw. 12 dB/Oktave strebt die akustische Phase in Richtung +90 bzw. +180° (und erreicht sie auch, wenn der Anstieg über einen längeren Frequenzbereich erfolgt).
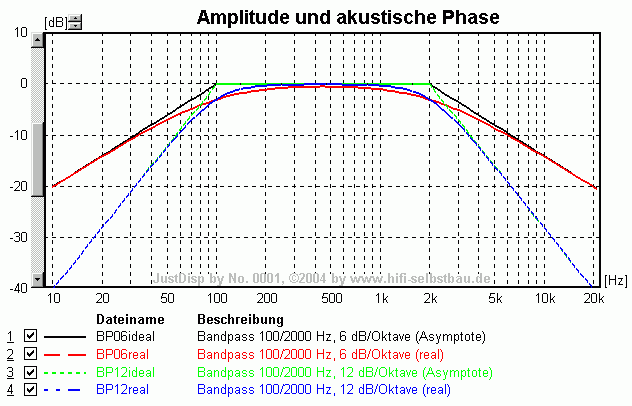
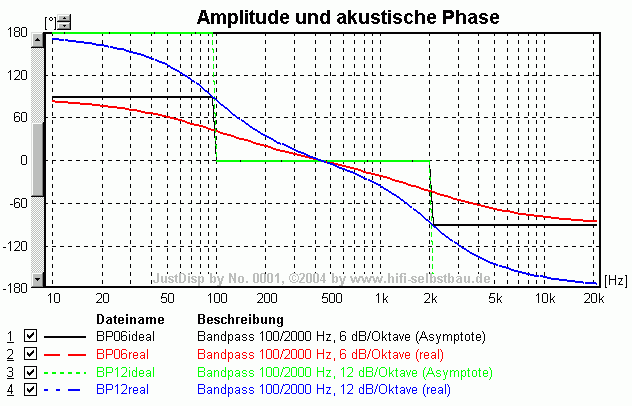
- während sich der Mitteltöner im Bereich von 500 bis 1000 Hz noch mitten in seinem Übertragungsbereich befindet (akustische Phase 0°) hat der Hochtöner unterhalb seiner Resonanzfrequenz einen Pegelanstieg von 12 dB/Oktave, seine akustische Phase strebt also gegen 180° -> die relative akustische Phase (aus Sicht des Mitteltöners für den Hochtöner) strebt gegen +180° für tiefe Frequenzen und sollte bei der Resonanzfrequenz etwa +90° betragen
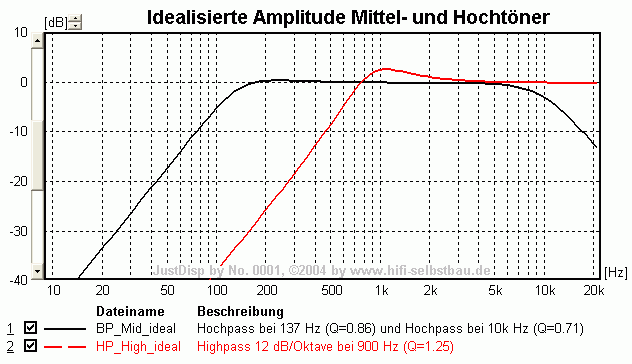
- im Bereich 1000 bis 5000 Hz ist der Mitteltöner immer noch mitten in seinem Übertragungsbereich (akustische Phase 0°), der Hochtöner auch. Daher müsste die relative akustische Phase eigentlich 0° sein wenn das Mikrofon gleich weit vom akustischen Zentrum der Einzelchassis entfernt wäre. Sobald der virtuelle Schallentstehungsort (in BoxSim mit SEO bezeichnet) nicht gleich weit vom Mikrofon entfernt ist kommt ein akustischer Phasenwinkel aus der Laufzeitdifferenz zustande. Im folgenden Bild wurden die verschiedenen Einflüsse mit idealisierten Wandlern synthetisiert:
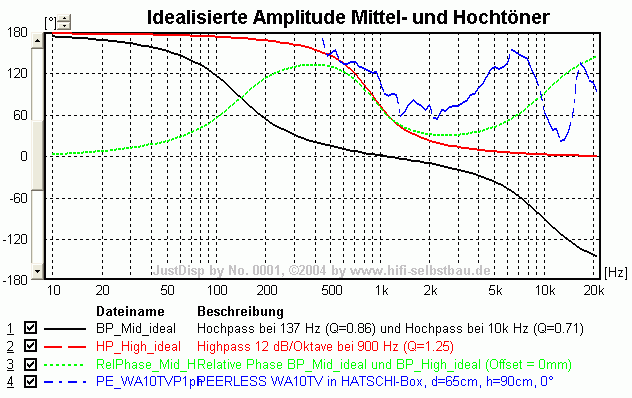
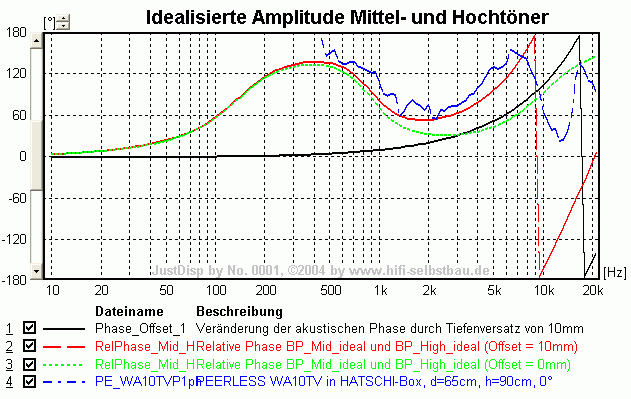
- die berechnete Phase lässt sich durch die relative akustische Phase idealisierter Chassis (identisches Fc und Qtc) und einen Tiefenversatz des Hochtöners von 10mm im Bereich von 500 bis 7000 Hz weitestgehend erklären! Damit ist mehr als eine Oktave unter- und oberhalb der Trennfrequenz von 2500 Hz eine korrekte Berücksichtigung der relativen akustischen Phase möglich! Abweichungen darüber sind sicherlich auf das nicht ideale Verhalten des Mitteltöners zurückzuführen (Resonanz bei 6.5 kHz).
Simulationsergebnisse:
Es wurden verschiedene Simulation der im Workshop "Entwicklung von passiven Frequenzweichen" behandelten HATSCHiBox mit Lasip durchgeführt. Dabei wurden verschiedene Varianten des Hochtöner-Datensatzes miteinander verglichen:
| Bezeichnung | Eigenschaften |
| PE_WA10TVP1 | keine Berücksichtigung der akustischen Phase |
| PE_WA10TVP1ph | Berücksichtigung der akustischen Phase wie berechnet (s.o.) |
| PE_WA10TVP1-ph | Berücksichtigung der akustischen Phase mit negativem Vorzeichen. Dies entspricht der Beaufschlagung des Mitteltöners mit der ursprünglich berechneten akustischen Phase |
Darüber hinaus wurde der Hochtöner ggf. verpolt (im Diagramm erkennbar an der Bezeichnung +/- bzw. -/+). Die "reale" Box klang in der Stellung "-/+" (also gegenüber dem Bass verpolt, am gleich gepolt wie der Mitteltöner) am besten und zeigt dort auch die besten Messwerte. Schließlich wurde auch noch ein virtueller Tiefenversatz von 2 cm eingefügt.
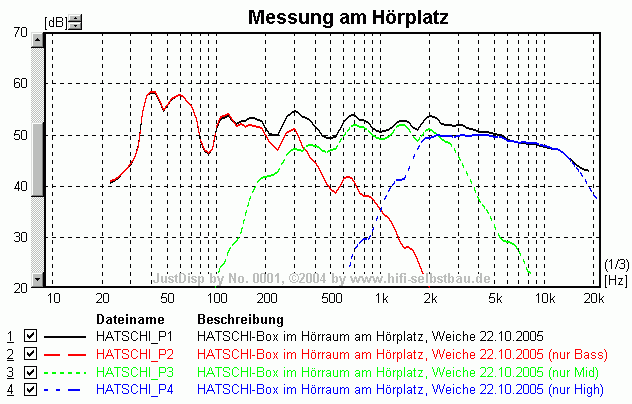
Hier zunächst die Messung am Hörplatz. Durch die große Entfernung von 3 m ergibt sich ein kontinuierlicher Abfall zu hohen Frequenzen hin, die aus der Bündelung der Chassis und dem Abfall der Nachhallzeit zu hohen Frequenzen hin resultiert.
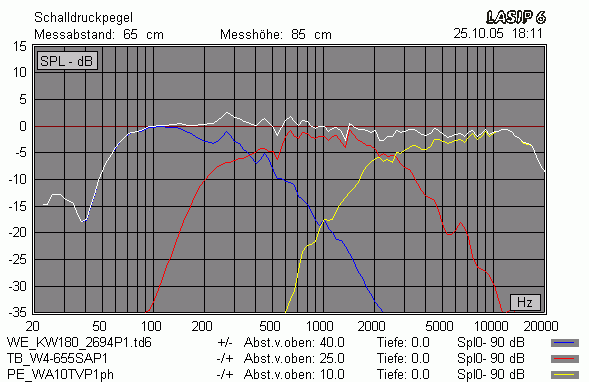
So stimmen Messung und Simulation gut überein (akustische Phase berücksichtigt)
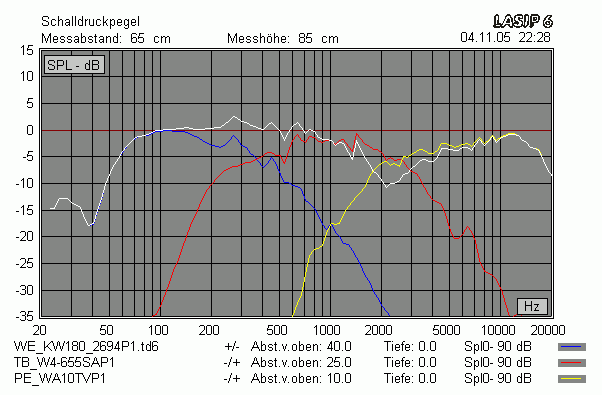
Hier stimmen Messung und Simulation gar nicht überein (akustische Phase nicht berücksichtigt)
Erst durch eine zusätzliche Verpolung sieht es wieder einigermaßen gleich aus
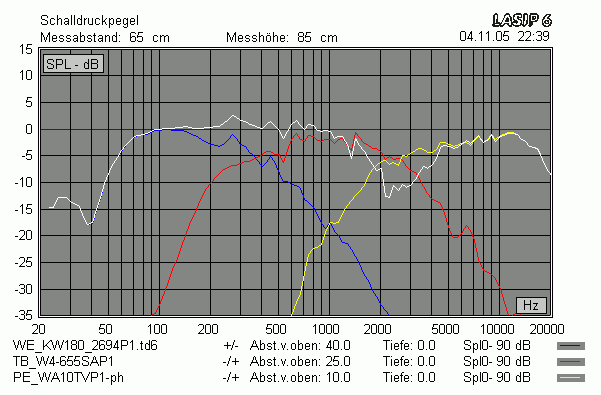
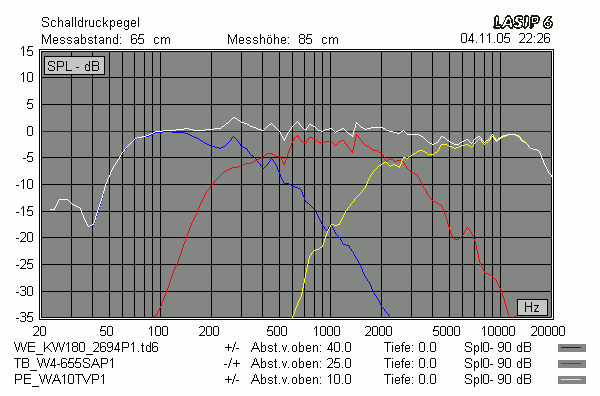
Hier stimmen Messung und Simulation gar nicht überein (akustische Phase mit negativem Vorzeichen berücksichtigt)
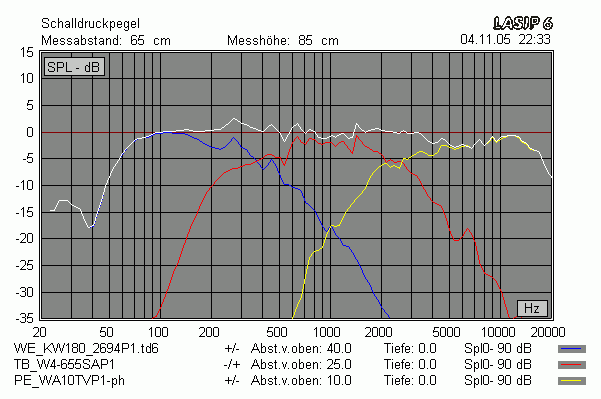
Erst durch eine zusätzliche Verpolung sieht es wieder einigermaßen gleich aus
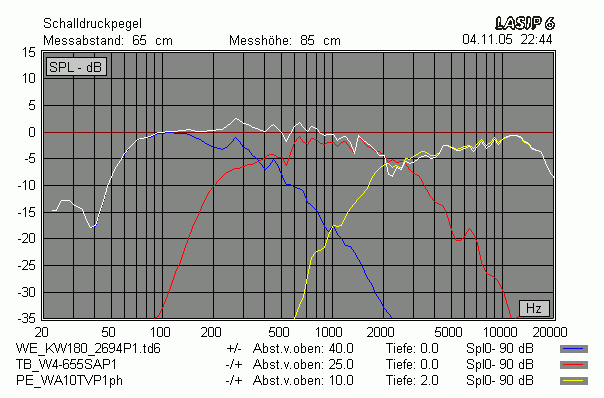
Und hier wurde der Hochtöner virtuell um 2 cm weiter nach hinten verschoben -> nun ergibt sich ein breiter Einbruch!