Wenn man verschiedene Musikkonserven über dieselben Lautsprecher abhört kann es passieren, dass bei einem Stück der Bassbereich "zu schlank" wiedergegeben wird, beim anderen "zu voll". Bei einem Stück ist das Klavier/Saxophon/Becken zu sehr im Vordergrund, beim anderen klingt es zu dumpf. Da stellt sich die Frage: was ist nun "richtig"?
Eigentlich hätte die Frage lauten sollen:
- wie viel davon liegt an der Aufnahme und
- wie viel an der Wiedergabe?
Die "harte" Tour:
Eine Methode, z.B. die Bassfülle einer Musikkonserve zu "objektivieren" ist, sich diese auf möglichst vielen Anlagen in möglichst vielen Räumen anzuhören und ein wenig Statistik zu machen. Dummerweise ist diese Vorgehensweise äußerst zeitaufwändig und vom Wohlwollen derer abhängig, die ihr Wiedergabesystem zur Verfügung stellen . . .Wenn man dies z.B. mit der CD "Holy Cole Trio / Temptation" macht wird man feststellen, dass die CD fast immer VIEL zu voll im Bassbereich wiedergegeben wird. Da ist es wahrscheinlicher, dass die Aufnahme zu basslastig ist, als dass fast ALLE Wiedergabesysteme zu basslastig sind. OK, diese CD wird also "richtig" wiedergegeben wenn sie "zu voll" im Bass klingt. Aber wie "zu voll" soll sie denn klingen? Oder besser: welche Musikkonserve muss denn "voll aber trotzdem knackig" klingen oder welche darf auf gar keinen Fall voll klingen? Idealerweise hätte man ja einen kleinen Fundus an CDs, die es erlauben z.B. den Bereich "Basswiedergabe" abzugrenzen.
Dummerweise besteht Musik aber noch aus anderen Frequenzbereichen, so dass man hier ähnlich vorgehen müsste. Wir haben uns daher unsere persönliche Test-CD zusammengestellt. Jedes der Stücke richtet die akustische Lupe auf einen bestimmten Bereich und erlaubt eine schnelle Einstufung "zu viel" / "ungefähr richtig" / "zu wenig". Wiedergabesysteme, die alle Checks mit "ungefähr richtig" bestehen, liegen in einem recht engen Korridor, in dem es kein falsch oder richtig mehr gibt sondern nur noch Geschmacksnuancen.
| Nr | Gruppe | Titel | CD | Jahr | Worauf achten |
| 1 | Bobby McFerrin | Blackbird | The Voice | 1984 | Glaubwürdige Stimme bzw. Geräusche (z.B. Luftholen, Klatschen); tiefe Lagen der Stimme dürfen nicht "dröhnen" |
| 2 | Jefferey Smith | Eleanor Rigby | A Little Sweeter | 1997 | Sehr (charakter-) volle Stimme mit viel "Luft", Klavier dumpf im Hintergrund |
| 3 | The King's Singers | Back In The U.S.S.R. | The Beatles Collection | 1986 | "Walking Bass" darf nicht zu fett sein, muss aber schieben und sich nach "Stimme" anhören; einzelne Einwürfe müssen leicht zu orten sein |
| 4 | Vocaleros | Superstition | Vocaleros | 1997 | Das muss sehr "knackig" klingen, darf aber auch noch nicht "nerven" (laute Frauenstimme); jeder einzelne Einwurf muss einfach zu orten sein |
| 5 | Brent Lewis | Mumbo Jumbo | Pulse . . . Where The Rhythm Begins | 1995 | Extrem breite räumliche Staffelung (dank? Studiotechnik, denn Brent hat alle Instrumente alleine gespielt), einfach zu orten; die Trommeln müssen Druck machen aber trotzdem knackig klingen |
| 6 | Talking Horns | Johann, der Tango kommt | Fisch im Wasser | * | Nur mit 2 Mikros aufgenommen; die "Präsenz" der Instrumente ist schwer hinzubekommen |
| 7 | Oscar Peterson | Dream Of You | Reunion Blues | 1972 | Bass ganz außen links, der Jazzbesen muss "körnig" aber dezent kommen, das Vibraphon ist SEHR breit (einzelne Töne müssen nachverfolgbar sein, auch in der Mitte) mit teilweise "bösen" Anschlägen, dumpfes Klavier darf nicht zugematscht sein |
| 8 | The Oscar Peterson Trio | You Look Good To Me | We Get Requests | 1965 | Berüchtigt ist die Triangel und der erst gestrichene, dann gezupfte Bass, der an keiner Stelle dröhnen darf |
| 9 | Melissa Walker | I'm A Fool To Want You | May I Feel | 1997 | Sehr räumlich ohne allzu viel "Pseudo"-Hall |
| 10 | Jennifer Warnes | Somewhere, Somebody | The Hunter | 1992 | Sehr breiter Pseudoraum, beide Sänger mittig (achten sie auf deren räumliches Wechselspiel) |
| 11 | Keb' Mo' | Just Like You | Just Like You | 1996 | Sehr erdig, die (Mit-)sänger müssen auseinander gehalten werden |
| 12 | Holly Cole | Jersey Girl | Temptation | 1995 | Sehr dicker Bass, alle Instrumente sehr dezent, Stimme voll, eher geknurrt |
| 13 | Mighty Sam McClain | Too Proud | Give It Up For Love | 1993 | Sehr spitzes Schlagzeug, auch bei lauten Passagen nicht nervig (Sänger bleibt unbeirrt) |
| 14 | Marla Glen | Personal | This Is Marla Glen | 1993 | Kehlige, dunkle Stimme, blitzblank geputzte Trompeten, fetter Bass, ungewöhnliche Instrumentierung (Akkordeon etc.), macht Lust auf mehr |
| 15 | Hugh Massekela | Stimela | Hope | * | Fortestellen müssen mit Druck kommen, realistische Stimme |
| 16 | Yello | Tied Up | Flag | 1988 | Hier fliegen die akustischen Fetzen; sehr knackige Soundcollage der Schweizer Soundtüftler -> da muss die Post abgehen! |
Die "weiche" Tour:
Nun mag nicht jeder die obige Musik, teilweise sind die CDs gar nicht mehr im Handel und außerdem hat man ja selber seit einiger Zeit seine persönliche Test-CD zusammengestellt. Und jetzt stellt sich die Frage: wie müsste die denn klingen? Dabei kann das Programm WaveAnalyzer helfen, dass sich auf der HiFi-Selbstbau Test-CD befindet. Was kann WaveAnalyzer?- gibt grundlegende Informationen zu einer WAV-Datei
- ermittelt für jeden Kanal statistische Kenngrößen (Min. Max, RMS etc.)
- führt eine spektrale Analyse für jeden Kanal durch
Erste Schritte mit WaveAnalyzer:
Nach Starten des Programms erscheint erst mal ein Dialog zur Auswahl einer WAV-Datei (oder mehrerer, z.B. alle Tracks einer CD):
Hinweis: Wie man von einer Audio-CD WAV-Dateien erzeugt steht im Artikel Musik "verstehen" mit GoldWave: Grundlagen.
Wie man sieht ist das Programm in englischer Sprache gehalten. Da es aber kaum Menüpunkte gibt dürfte das nur wenig stören . . . Als nächstes will das Programm wissen, mit welchen Analyseparametern gearbeitet werden muss. Die Standardeinstellung ist:
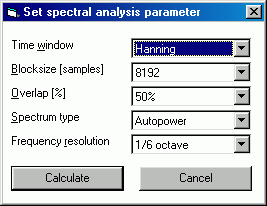
Die Parameter sind für die Analyse von CDs optimiert. Was da im Einzelnen passiert kann der technisch Interessierte gerne weiter unter nachlesen (muss er aber nicht).
Danach erscheint folgender Bildschirm:
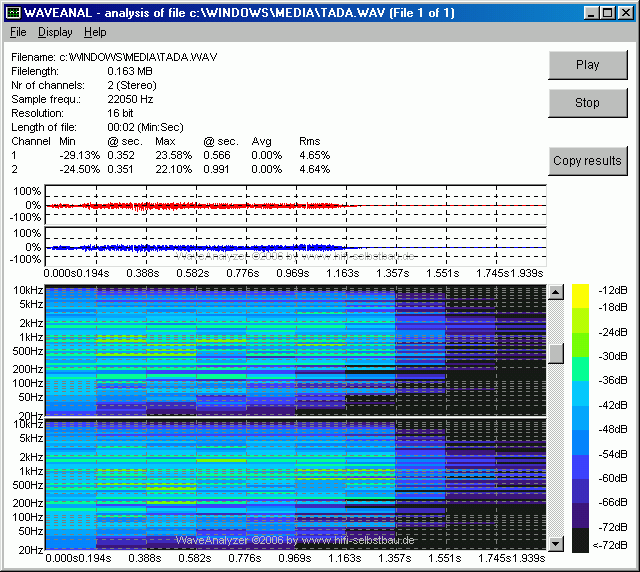
Hinweis: Die aktuelle Version von WaveAnalyzer ist für eine Bildschirmauflösung von 1024 x 768 Pixel optimiert. Bei anderen Bildschirmgrößen gerät die Darstellung evtl. etwas "durcheinander".
Der Bildschirm lässt sich grob in 3 Teile untergliedern:
- Der obere Teil enthält Angaben zur WAV-Datei (Name, Größe, Kanäle, Auflösung, Länge etc.) sowie eine statistische Auswertung des Zeitsignals für jeden Kanal getrennt (Min/Max mit Angabe der Position, Avg und RMS). Der lineare Mittelwert Avg sollte < +/- 1% sein, ansonsten gab es einen Gleichspannungsoffset in der Aufnahmekette. Der energetische Mittelwert RMS wird weiter unten bzw. im Artikel Musik "verstehen" mit GoldWave: Grundlagen erklärt.
- Der mittlere Teil stellt das komplette Zeitsignal dar (rot/oben - linker Kanal, blau/unten - rechter Kanal). Die Zeitachse verläuft von links nach rechts.
- Der untere Teil stellt die Frequenzanalyse des Zeitsignal dar (oben - linker Kanal, unten - rechter Kanal). Die Zeitachse verläuft wieder von links nach rechts. Die Frequenzachse verläuft jeweils von unten nach oben. Der Pegel wird als Farbe dargestellt, die Zuordnung ist aus dem Farbbalken rechts erkennbar.
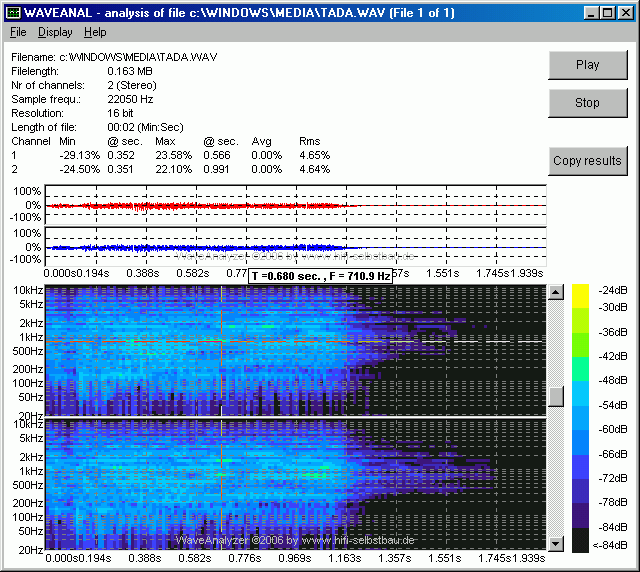
Mit dem vertikalen Schieberegler rechts unten kann man den Pegelbereich verändern (0 dB entspricht dem Pegel eines voll ausgesteuerten Sinussignals). Wenn man die Maus über den unteren Bildschirmbereich führt wird die aktuelle Mausposition angezeigt (Info in der Fenstermitte).
Ergebnisse von WaveAnalyzer:
Das sieht zwar alles ganz nett aus, aber wirklich ablesen kann man dort nix. Wenn man auf die Schaltfläche "Copy results" drückt (rechts oben) werden die Ergebnisse in die Zwischenablage kopiert:
Die Ergebnisse sehen folgendermaßen aus:
- Zunächst wird der obere Teil des Fenster kopiert:
Filename: c:\WINDOWS\MEDIA\TADA.WAV
Filelength: 0.163 MB
Nr of channels: 2 (Stereo)
Sample frequ.: 22050 Hz
Resolution: 16 bit
Length of file: 00:02 (Min:Sec)
Channel Min @ sec. Max @ sec. Avg RMS
1 -29.13% 0.352 23.58% 0.566 0.00% 4.65%
2 -24.50% 0.351 22.10% 0.991 0.00% 4.64% - Dann werden die Analyseparameter angegeben:
Analysis parameters:
Block size: 1024
Number of blocks 164
Offset per block: 254 Samples
Time window: Hanning
FrequencyResolution: 1/6 octave - Schließlich wird der energetische Mittelwert und der Maximalwert für jeden Kanal angegeben. Ganz zum Schluss wird noch der unbewertete und A-bewertete Summenpegel ausgegeben (Näheres dazu weiter unten).
Please note that 0 dB corresponds to full scale deflection of the wave file!
F [Hz] Ch1_Avg [dB] Ch1_Max [dB] Ch2_Avg [dB] Ch2_Max [dB]
19.95 -79.40 -68.17 -78.36 -67.58
22.39 -77.86 -66.44 -76.56 -65.16
25.12 -77.19 -65.75 -75.86 -64.26
28.18 -76.69 -65.25 -75.36 -63.76
31.62 -76.19 -64.75 -74.86 -63.26
35.48 -75.69 -64.25 -74.36 -62.76
39.81 -75.19 -63.75 -73.86 -62.26
44.67 -71.12 -58.86 -70.05 -57.82
50.12 -70.13 -57.73 -69.09 -56.81
56.23 -69.63 -57.23 -68.59 -56.31
63.10 -67.19 -55.99 -66.97 -55.64
70.79 -64.10 -53.16 -64.67 -53.02
79.43 -63.60 -52.66 -64.17 -52.52
89.13 -63.50 -51.11 -64.29 -51.91
100.0 -63.10 -50.39 -63.95 -51.38
112.2 -61.99 -51.04 -63.43 -52.90
125.9 -59.85 -51.21 -62.14 -53.04
141.3 -56.93 -47.97 -60.13 -50.59
158.5 -60.38 -50.65 -63.08 -54.51
177.8 -62.19 -53.43 -63.57 -54.69
199.5 -58.76 -49.80 -58.78 -49.95
223.9 -60.67 -51.45 -60.39 -52.07
251.2 -59.44 -51.47 -58.65 -51.86
281.8 -57.21 -49.30 -56.23 -48.94
316.2 -59.54 -50.40 -59.32 -51.45
354.8 -59.63 -50.75 -59.70 -51.65
398.1 -55.04 -46.94 -57.18 -48.34
446.7 -60.59 -51.53 -61.85 -52.38
501.2 -57.01 -49.06 -57.91 -49.96
562.3 -56.52 -48.83 -56.88 -49.11
631.0 -55.64 -47.71 -56.08 -48.00
707.9 -55.73 -48.21 -55.27 -46.35
794.3 -53.81 -45.97 -53.90 -45.92
891.3 -61.20 -51.95 -61.63 -54.25
1000 -55.72 -48.38 -54.41 -46.49
1122 -57.03 -48.28 -54.46 -47.60
1259 -58.58 -51.46 -58.17 -50.08
1413 -61.20 -53.96 -60.11 -51.55
1585 -54.25 -46.55 -54.07 -45.46
1778 -64.36 -57.08 -64.26 -56.64
1995 -55.33 -49.82 -55.90 -49.42
2239 -59.41 -52.07 -58.09 -51.34
2512 -62.71 -57.04 -60.87 -54.98
2818 -67.24 -59.82 -66.74 -58.41
3162 -59.01 -52.37 -58.21 -51.20
3548 -69.05 -62.15 -68.82 -61.46
3981 -63.02 -56.09 -63.76 -57.23
4467 -68.54 -60.61 -67.78 -60.46
5012 -65.76 -58.14 -65.61 -58.14
5623 -73.90 -64.70 -73.63 -65.41
6310 -67.95 -62.10 -69.39 -62.76
7079 -71.73 -64.13 -71.59 -64.69
7943 -74.88 -67.52 -75.20 -66.13
8913 -77.05 -69.15 -77.13 -68.76
10000 -79.36 -70.45 -78.95 -68.66
Sum (linear) -42.85 -42.85
Sum (A-weighted) -44.71 -44.33
Der Inhalt der Zwischenablage ist übrigens so formatiert, dass er mit "Bearbeiten / Einfügen" (oder Strg+V) direkt in eine Tabellenkalkulation (wie z.B. EXCEL®) eingelesen werden kann.
Hinweis: Wer die deutsche Ländereinstellung verwendet wird bei den statistischen Angaben Probleme mit dem Dezimalpunkt haben. Die übrigen Zahlen werden durch die Zwischenablage umgewandelt.
So, wenn man nun ein "richtiges" Musikstück analysieren würde könnte man erkennen:
- wie viel "Bass" auf der CD drauf ist (wie tief, ab wann, wie steiler Abfall etc.)
- bei welchen Frequenzen die maximale Energie auftritt
- wie hoch der Unterschied zwischen energetischem Mittelwert und maximalem Pegel (= spektrale Dynamik) in der jeweiligen 1/n Oktave ist
- etc.
Analyse unserer Hörtest-CD:
Das Ganze macht aber erst Sinn, wenn man mehrere Stücke oder Teile von Stücken analysiert. Wir haben das mal für unsere Hörtest-CD gemacht (linker Kanal):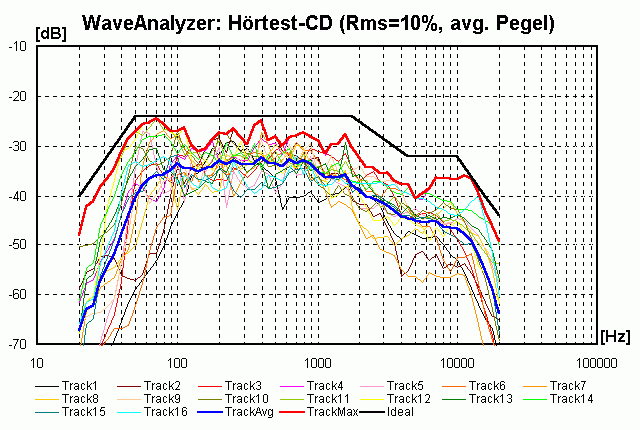
Hinweis: Keine Angst vor den vielen Kurven: es kommt vor allem auf die 3 dicken Linien an . . .
- die dünnen Kurven sind die mittleren Pegel der einzelnen Stücke. Wie man sieht ist bei der dünnen schwarzen Linie (Stück 1) unter 100 Hz kaum etwas los, das orange Stück 7 (Oscar Peterson / Dream of You) hat z.B. sehr wenig Energie oberhalb von 2 kHz (der Jazzbesen ist auf dem rechten Kanal)
- die dicke blaue Linie ist der energetische Mittelwert aller 16 Stücke. Hier kann man einen gewissen Trend erkennen
- einen ähnliche Trend kann man bei der dicken roten Linie erkennen, die die maximalen in irgendeinem Stück jemals auftretenden energetischen Mittelwert in einem 1/6 Oktavband zeigt
- die dicke schwarze Kurve versucht den Verlauf der dicken blauen bzw. roten Kurve durch einfache Geraden anzunähern
Demzufolge geht der Pegel unterhalb von 50 Hz rapide bergab (ca. -12 dB/Oktave). Oberhalb von 1.8 kHz gibt es eine "Treppe" (Steilheit ca. -6 dB/Oktave) von ca. -8 dB, oberhalb von 10 kHz geht es auch rapide bergab (ca. -12 dB/Oktave).
Hinweis: Das bedeutet nicht, dass diese Frequenzen nicht wichtig sind, es bedeutet nur, dass sie nicht so laut sind!
Eine solche Analyse gibt wertvolle Hinweise darauf, welches Chassis wie viel Energie abbekommt. So muss bei einem klassischen 2-Wege-System mit einer Trennfrequenz von 2000 Hz der Tief-Mitteltöner den Löwenanteil der Leistung in Schall umsetzen. Andererseits erkennt man, dass bei einer Erhöhung der Trennfrequenz auf z.B. 3 kHz der Hochtöner deutlich entlastet wird und dass die Steilheit des Hochpassfilters in diesem Bereich sehr wichtig ist!
Wenn man statt der energetischen Mittelwerte die maximal auftretenden Pegel nimmt, sieht das Bild sehr ähnlich aus:
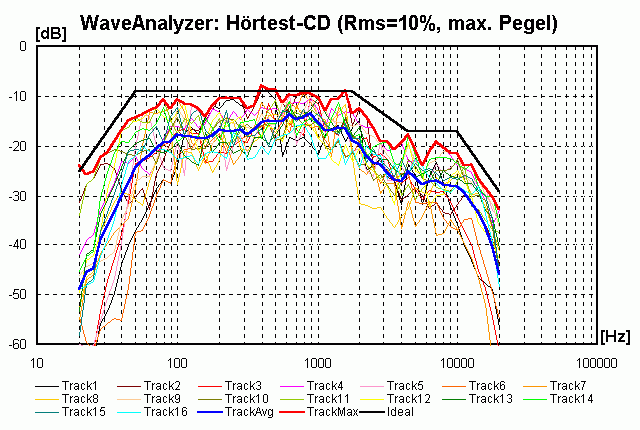
Hinweis: Keine Angst vor den vielen Kurven: es kommt vor allem auf die 3 dicken Linien an . . .
Die Kurven sind im wesentlichen um ca. 17 dB parallel verschoben, d.h. kurzfristig müssen 17 dB lautere Pegel "verkraftet" bzw. umgesetzt werden. Der Bereich von 400 bis 1000 Hz ist sogar um ca. 20 dB lauter als die mittleren Pegel, hier geht es also besonders dynamisch zu. Im Tiefbassbereich ist die Dynamik eher etwas geringer.
Spektrale Analyse - wie geht das? (nur für technisch Interessierte)In der WAV-Datei ist das Zeitsignal gespeichert, wir wollen aber wissen, welche Frequenzen darin vorkommen! Alle beteilgten Frequenzen zusammen bilden das Frequenzspektrum. Für die Umwandlung vom Zeit- in den Frequenzbereich verwendet man üblicherweise die FFT (Fast Fourier Transformation). Wenn man in die FFT einen Block von 2n Abtastwerten hineinsteckt werden daraus 2n/2 Frequenzlinien (jede mit Amplitude und Phase) berechnet. Da es hier vor allem um die Analyse von CD-Signalen geht zunächst mal ein paar "technische Daten":
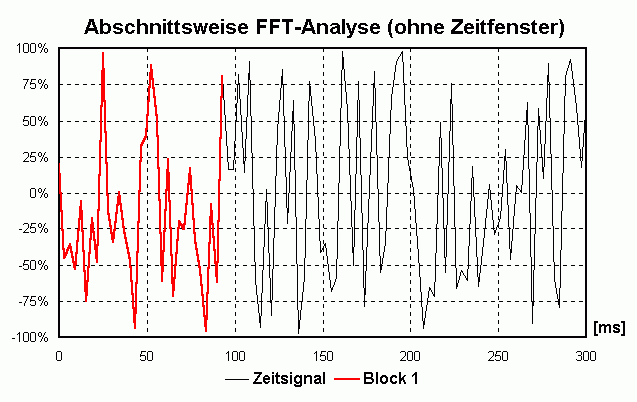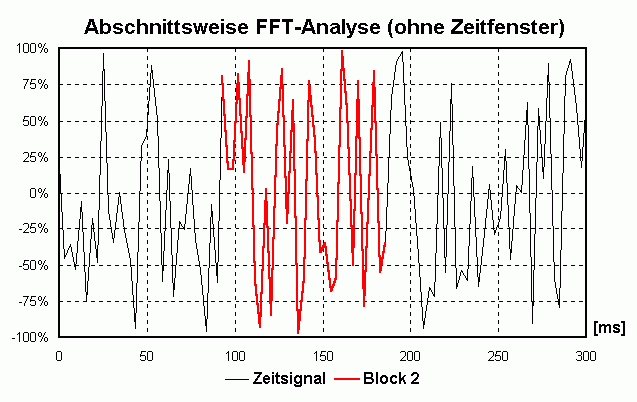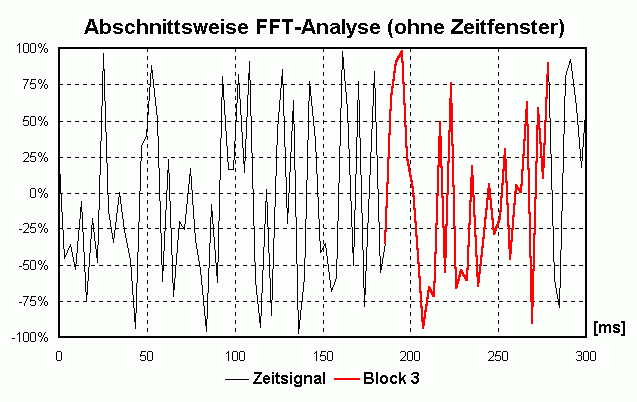
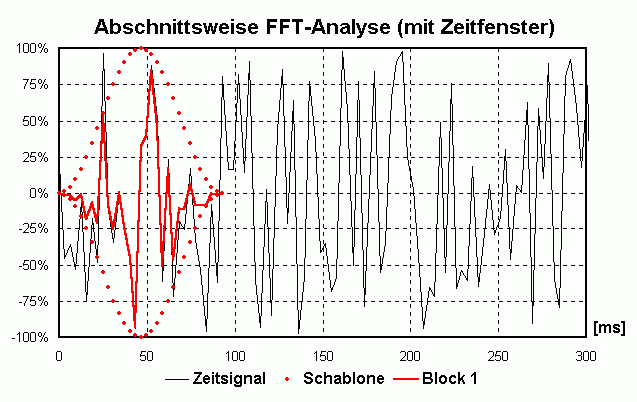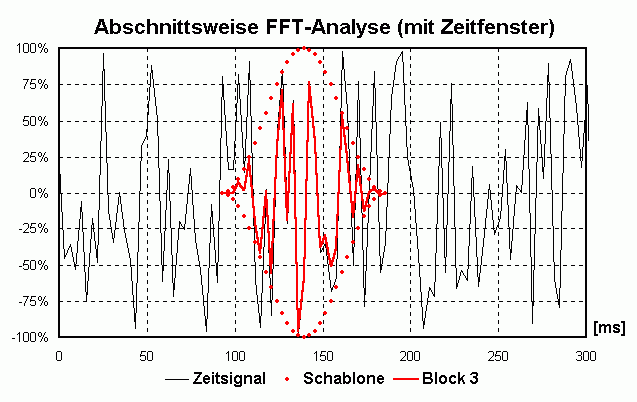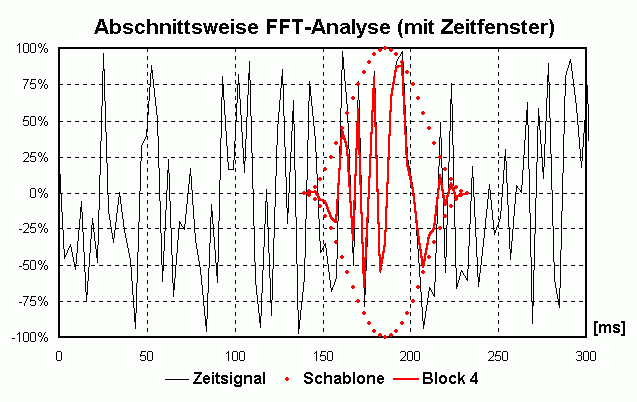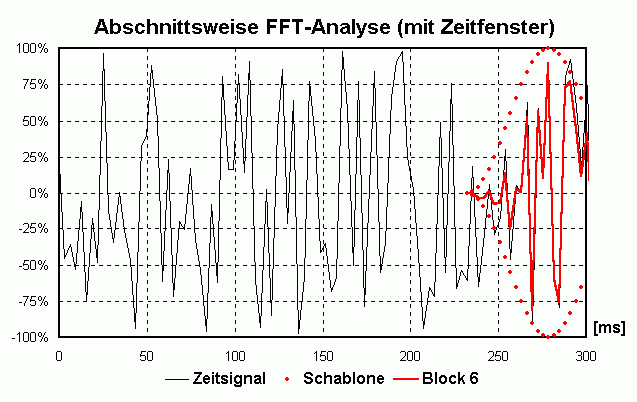
Die periodische Fortführung kann man sich so vorstellen, dass man den Block oft "kopiert" und dann "aneinander klebt". Wenn sich der Block etwa 10x pro Sekunde wiederholt kann die tiefste vorkommende Frequenz nur die sein, die sich auch 10x pro Sekunde wiederholt, also eine Frequenz von 10 Hz ([Hz] = [1/s]) hat. Auch Frequenzen von x · 10 Hz erfüllen diese Bedingung. Man spricht von einer Frequenzauflösung von 10 Hz. Beim "Aneinanderkleben" der einzelnen Blöcke kann es zu unschönen "Stoßstellen" kommen, die sich beim Anhören als "Knackser" outen würden und durch den Prozess des Zusammenklebens erst entstanden sind (und daher nicht dahin gehören). Um das zu vermeiden blendet man jeden einzelnen Block sanft von 0 auf 100% ein und von 100 auf 0% aus, man guckt also durch eine "Schablone" auf das Signal. Diese unterschiedliche Bewertung des Zeitsignals nennt man Zeitfenster (Englisch: time window). Da man im Leben nix geschenkt kriegt hat der Vorteil der knackfreien Aneinanderreihung auch Nachteile. Daher gibt es verschiedene Zeitfenster, die jeweils etwas andere Vor- und Nachteile haben. Bei WaveAnalyzer ist die Standardeinstellung das sog. HANNING-Fenster (Formel: W(t) = 0.5 + cos(2 · Pi · t/T)/2 mit T = Blocklänge und t von -T/2 bis +T/2). Dadurch geht an den Rändern leider Information "verloren" bzw. wird nicht zu 100% "verwertet". Deshalb verschiebt man die Schablone für den nächsten Block nicht eine komplette Blocklänge weiter sondern z.B. nur 50% davon. Dadurch "überlappen" sich zwei aufeinanderfolgende Blöcke um 50% (Overlap = 50%). Dadurch wird jetzt an anderer Teil des ursprünglichen Signals "beleuchtet" und analysiert. Die folgende Animation verdeutlicht das prinzipielle Vorgehen:
|
Kompromiss zwischen Zeit- und Frequenzauflösung
Im Bassbereich < 100 Hz ist eine Frequenzauflösung von 10.77 Hz (> 10%) nicht so toll, im Hochtonbereich > 10000 Hz dagegen völlig überkandidelt (< 0.1%). Ein Klavier kann ja auch nur bestimmte (Grund-) Töne erzeugen: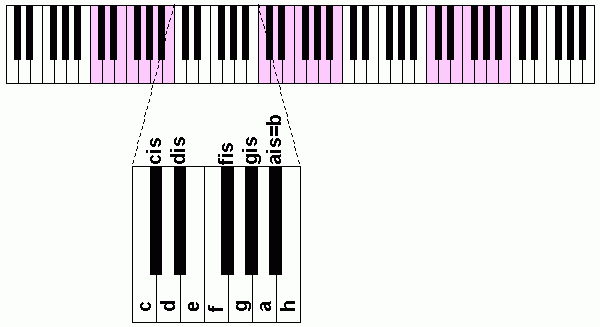
Dort wiederholt sich die Tastenanordnung alle 12 Tasten (7 weiße und 5 schwarze), danach wird derselbe Ton eine Oktave höher gespielt, das entspricht der doppelten Frequenz. Die Stufung dazwischen ist prozentual ungefähr gleich, der Faktor beträgt ungefähr 21/12 = 1.0595, jeder Ton ist also etwa 6% höher als der Vorhergehende. Wenn unsere Frequenzanalyse diese (Oktav-) Auflösung hätte wäre das also angemessen.
Wie wir oben gesehen haben bedeutet eine hohe Frequenzauflösung aber eine lange Beobachtungszeit bzw. große Blockgröße:
Frequenzauflösung dF [Hz] = Abtastfrequenz Fs [Hz] / Blockgröße
Hier ist also ein Kompromiss gefragt zwischen genauer Frequenzerkennung und Unterdrückung von kurzzeitigen Signalspitzen durch zu lange Mittelung. Als sinnvoller Kompromiss hat sich eine Blockgröße von 8192 Abtastwerten und eine Auflösung von 1/6 Oktave erwiesen. Bei Verwendung des HANNING-Zeitfensters und einer Überlappung von 50% (Standardeinstellung von WaveAnalyzer) "beleuchtet" man jeweils
8192/44100 · 50% = ca. 0.1 s
mit mehr als 50%. Die Frequenzauflösung beträgt
44100 / 8192 = 5.38 Hz.
Die unterste 1/6 Oktave, bei der der Abstand der nächsten 1/6 Oktave genau dem Abstand der Frequenzlinien entspricht wäre
5.383 / (1-21/6) = 43.7 Hz,
d.h. ab der 1/6 Oktave mit der Mittenfrequenz von 40 Hz wäre die Frequenzauflösung der FFT ausreichend um daraus eine 1/6 Oktave zu berechnen.
Der niedrigste Ton des Klaviers (A2) liegt bei etwa 27.5 Hz (a1 = 440 Hz), der tiefste Ton des Elektro- oder Kontrabass (E2) bei 41.2 Hz. Instrumente wie die Orgel oder elektronisch erzeugte Klänge (Synthesizer) reichen noch tiefer.
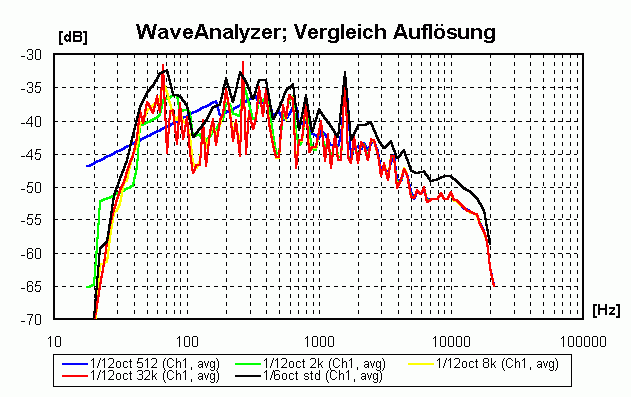
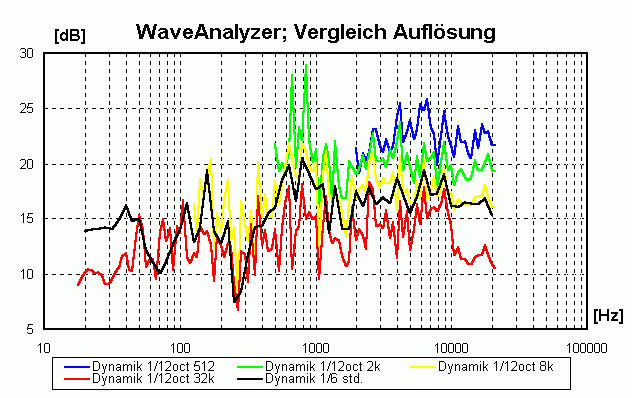
Gut, besser am besten! (nur für technisch Interessierte)Idealerweise würde man ein Stück im Bereich der tiefen Frequenzen mit einer höheren Frequenzauflösung analysieren. Um eine 1/12-Oktavauflösung bis herunter zu 27.5 Hz zu erzielen wäre eine Frequenzauflösung von mindestens27.5 · (1-21/12) = 1.64 Hz nötig. Die Blockgröße würde dann 2x = 44100 / 1.64 -> x = 15 -> Blockgröße = 32768 betragen, das entspricht einer Länge von 32768 / 44100 = 0.742 Sekunden, d.h. über diesen Zeitraum würde die im Block enthaltene Energie gemittelt. Das ist für mittlere und hohe Frequenzen zu viel, so dass die FFT für diese Frequenzbereiche mit geringeren Blockgrößen wiederholt werden müsste. Einen Vergleich der
Hinweis: die 1/6-Oktav-Ergebnisse müssten 3 dB "lauter" sein, da ja in die "breitere" 1/6 Oktave doppelt soviel Energie passt!
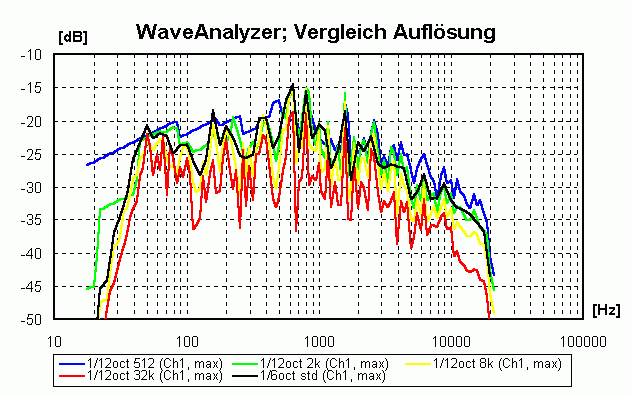
|
Zusammenfassung der Erkenntnisse zum Thema Zeit- und Frequenzauflösung:
- Die Standardeinstellungen von WaveAnalyzer liefern bei minimalen Berechnungsaufwand ein Maximum an brauchbaren Informationen!
- Bei einer optimierten 4-fach Auswertung ist sowohl im Bassbereich eine höhere Frequenzauflösung als auch im Hochtonbereich eine höhere Zeitauflösung möglich
- Die spektrale Dynamik (Unterschied zwischen mittlerem und maximalem Spektrum) wird mit der Standardeinstellung im mittleren und oberen Frequenzbereich um ca. 6 dB unterschätzt
Weitere Ergebnisse von WaveAnalyzer
Bei der Zusammenstellung von Stücken verschiedener CDs zu einem Sampler tritt immer wieder das Problem auf, dass die einzelnen Stücke unterschiedlich laut sind und man bei der Wiedergabe ständig am Lautstärkeregler drehen muss. Der bei vielen Brennprogrammen zu findende Schalter "normalize amplitude" verspricht zwar die Lautstärke zu "normalisieren", dies betrifft aber nur den Maximalwert des Zeitsignals. Wie wir schon im Artikel Musik "verstehen" mit GoldWave: Grundlagen gesehen und gehört haben ist dieser aber ungeeignet die subjektiv empfundene Lautstärke zu beschreiben.Durch Anwendung von Dynamikkompressoren gelingt es heute, die subjektiv empfundene Lautstärke bei gleichem Maximalpegel zu erhöhen. Unter der Annahme, dass die spektrale Verteilung ähnlich ist kann der energetische Mittelwert oder RMS-Wert als Maß für die relativen, subjektiven Lautstärkeunterschiede verwendet werden. Eine 2. Größe, die WaveAnalyzer zur Verfügung stellt, ist der A-bewertete Summenpegel. Summenpegel bedeutet, dass die Energie aller Frequenzen zusammengefasst wird. Die A-Bewertung kompensiert dabei ungefähr die unterschiedlich empfundene Lautstärke bei verschiedenen Frequenzen. Die Differenz der A-bewerteten Summenpegel ist daher ein gutes Maß für die relativen Lautstärkeunterschiede besonders dann, wenn 2 Stücke eine stark unterschiedliche spektrale Verteilung haben. Die Zusammenhänge zeigt das folgende Bild:
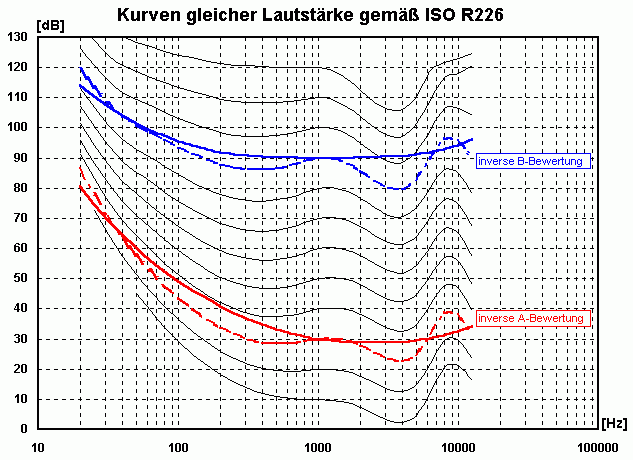
Hinweis: Es gibt verschiedene Untersuchungen zu dem Thema, die oft zu unterschiedlichen Ergebnissen kamen. Das hat mit der Versuchsdurchführung, dem Alter und Geschlecht sowie dem Kulturkreis (!) zu tun. Die Kurven gleicher Lautstärke nach Zwicker haben jedoch als einzige den Ritterschlag durch einen Normungsausschuss erhalten.
Wie muss ich denn das verstehen? Per Definition wird ein Sinuston von 1 kHz mit einer objektiven Lautstärke von z.B. 50 dB auch 50 Phon laut empfunden. Für denselben Lautstärkeeindruck von 50 Phon ist bei einem Sinuston von 500 Hz nur ein objektiver Schalldruck von 47 dB nötig, bei dieser Frequenz ist das Gehör also etwas empfindlicher. Die maximale Ohrempfindlichkeit liegt - bei dieser Lautstärke - bei ca. 4 kHz (bei hohen Lautstärken > 100 Phon ändert sich die Frequenz der maximalen Ohrempfindlichkeit auf etwa 3.5 kHz).
Für tiefe Frequenzen unter 100 Hz ist das menschliche Ohr besonders unempfindlich, d.h. hier muss besonders viel objektiver Schalldruck erzeugt werden um eine Lautstärkeempfindung hervorzurufen. Wenn wir bei der 50 Phon-Kurve bleiben muss bei 100 / 50 / 25 Hz ein objektiver Schalldruck von 59 / 71 / 88 dB erzeugt werden um gleich laut empfunden zu werden wie ein 50 dB Sinuston von 1 kHz. Diese Tatsache ist auch der Grund, warum man bei Bässen höhere objektive Lautstärken subjektiv besser "genießen" kann. "Leider" ist das aber für den Lautsprecher und den Verstärker Schwerstarbeit. Daher trennt sich bei solchen Passagen die (Anlagen-) Spreu vom Weizen . . .
Hinweis: Die Tatsache, dass das menschliche Ohr bei tiefen Frequenzen weniger empfindlich ist bedeutet übrigens nicht, dass man einen Lautsprecher oder Verstärker mit Bassanhebung benötigt. Wenn Aufnahme und Wiedergabe linear sind (und in Originallautstärke abgehört wird) ist alles im Lot!
Für eine Lautstärkeempfindung von 60 Phon muss für die meisten Frequenzen ein 10 dB höherer Schalldruckpegel erzeugt werden, es kommen also keine weiteren Nichtlinearitäten hinzu. Lediglich unterhalb von 200 Hz sind geringere objektive Schalldruckerhöhungen nötig. Für kleinere Lautstärken fängt dieser Effekt bei noch höheren Frequenzen an. Dies war vor vielen Jahren die Begründung, warum HiFi-Geräte sog. Loudness-Tasten zur gehörrichtigen Lautstärkekorrektur hatten: wenn man ein Musikstück leiser als in Originallautstärke abhörte wurde die unterschiedliche Ohrempfindlichkeit mehr oder weniger gut ausgeglichen. Da der Wirkungsgrad der Lautsprecher und die Aussteuerung der Signalquelle nicht bekannt konnte das natürlich nur eine grobe Schätzung sein weil man nicht genau wusste wo man sich in der obigen Grafik befand. Außerdem unterscheidet sich z.B. der Klang eines leise oder laut gespielten Klaviers stark, was bei zu leisem Abspielen und Gebrauch der Loudness-Taste zu einer unnatürlichen Klangfarbe führte. Mittlerweile verzichtet man aus verschiedenen Gründen lieber auf diese Korrektur und empfiehlt, möglichst in Originallautstärke zu hören ;-)
Wie erreicht man denn nun, dass bei einer persönlichen Zusammenstellung alle Stücke gleich laut empfunden werden?
- Wenn die spektrale Zusammensetzung sehr ähnlich ist sollten alle Stücke auf den gleichen RMS-Wert gebracht werden. Der RMS-Wert kann entweder kanalweise mit WaveAnalyzer oder gemittelt mit GoldWave ermittelt werden -> dies kann dazu führen, dass stark dynamikkomprimierte Stücke im Maximalpegel auf unter 50% reduziert werden müssen damit sie im Vergleich zu weniger stark komprimierten Stücken nicht zu laut empfunden werden!
- Ansonsten sollte der A-bewertete Summepegel aller Stücke identisch sein. Dieser wird nur von WaveAnalyzer in dB(A) berechnet. Um Hinweise für die zu ändernde Lautstärke in % zu bekommen muss der dB(A) 2delogarithmiert" werden (Pa(A) = 10(dB(A)/20)):
Beispiel Hörtest-CD:
| Stück | Max-Wert bzw. Min-Wert | RMS-Wert (gemittelt) | Summe [dB(A)] (gemittelt) | -> Druck [Pa(A)]* | RMS/Max | Druck/Max |
| 1 | 78.26 % | 4.86 % | -28.36 | 3.82% | 6.21% | 4.88% |
| 2 | 97.05 % | 12.06 % | -20.10 | 9.89% | 12.42% | 10.19% |
| 3 | 93.66 % | 8.96 % | -20.78 | 9.14% | 9.56% | 9.76% |
| 4 | 92.83 % | 16.84 % | -14.57 | 18.69% | 18.14% | 20.13% |
| 5 | 94.16 % | 6.93 % | -25.82 | 5.12% | 7.35% | 5.43% |
| 6 | 98.57 % | 6.67 % | -22.93 | 7.14% | 6.77% | 7.24% |
| 7 | 69.70 % | 8.82 % | -22.95 | 7.12% | 12.65% | 10.22% |
| 8 | 80.98 % | 8.73 % | -23.42 | 6.75% | 10.77% | 8.33% |
| 9 | 97.19 % | 8.58 % | -21.06 | 8.85% | 8.82% | 9.11% |
| 10 | 87.34 % | 10.45 % | -22.96 | 7.12% | 11.96% | 8.15% |
| 11 | 98.86 % | 10.51 % | -19.56 | 10.53% | 10.63% | 10.65% |
| 12 | 100.00 % | 9.32 % | -20.50 | 9.44% | 9.32% | 9.44% |
| 13 | 95.46 % | 7.12 % | -23.10 | 7.00% | 7.46% | 7.34% |
| 14 | 91.06 % | 13.47 % | -19.51 | 10.59% | 14.79% | 11.63% |
| 15 | 76.74 % | 4.45 % | -27.69 | 4.13% | 5.79% | 5.38% |
| 16 | 71.95 % | 5.91 % | -25.13 | 5.54% | 8.21% | 7.70% |
Angleichung der RMS-Werte: Die geringsten RMS-Werte weisen die Stücke 1 und 15 auf. Da der Maximalpegel 100% nicht übersteigen darf wird das Minimum von RMS/Max gesucht. Auf diesem RMS-Wert sind alle anderen Stücke zu bringen (Änderung der Lautstärke um X % mit GoldWave).
Angleichung der Pa(A)-Werte: Die geringsten Pa(A)-Werte weisen die Stücke 1 und 15 auf. Da der Maximalpegel 100% nicht übersteigen darf wird das Minimum von Pa(A)/Max gesucht. Auf diesem RMS-Wert sind alle anderen Stücke zu bringen (Änderung der Lautstärke um Y % mit GoldWave).
| Stück | RMSneu = 5.79 % | Pa(A)neu = 4.88% | ||||
| Faktor | Maxneu | Pa(A)neu | Faktor | Maxneu | RMSneu | |
| 1 | 119.18 % | 93.27 % | 4.55 % | 127.78% | 100.00% | 6.21% |
| 2 | 48.05 % | 46.63 % | 4.75 % | 49.37% | 47.91% | 5.95% |
| 3 | 64.68 % | 60.58 % | 5.91 % | 53.42% | 50.03% | 4.78% |
| 4 | 34.40 % | 31.93 % | 6.43 % | 26.13% | 24.26% | 4.40% |
| 5 | 83.64 % | 78.76 % | 4.28 % | 95.44% | 89.86% | 6.61% |
| 6 | 86.84 % | 85.60 % | 6.20 % | 68.42% | 67.45% | 4.56% |
| 7 | 65.71 % | 45.80 % | 4.68 % | 68.58% | 47.80% | 6.05% |
| 8 | 66.39 % | 53.76 % | 4.48 % | 72.35% | 58.59% | 6.31% |
| 9 | 67.55 % | 65.65 % | 5.98 % | 55.17% | 53.62% | 4.73% |
| 10 | 55.43 % | 48.41 % | 3.94 % | 68.62% | 59.93% | 7.17% |
| 11 | 55.09 % | 54.47 % | 5.80 % | 46.39% | 45.86% | 4.88% |
| 12 | 62.18 % | 62.18 % | 5.87 % | 51.73% | 51.73% | 4.82% |
| 13 | 81.35 % | 77.66 % | 5.70 % | 69.74% | 66.57% | 4.97% |
| 14 | 43.02 % | 39.17 % | 4.55 % | 46.13% | 42.00% | 6.21% |
| 15 | 130.31 % | 100.00 % | 5.38 % | 118.36% | 90.83% | 5.26% |
| 16 | 98.09 % | 70.58 % | 5.44 % | 88.10% | 63.39% | 5.20% |
Nach Angleichung der subjektiven Lautstärke über einen identischen RMS- oder Pa(A)-Wert streut der jeweils andere Wert nur noch um den Faktor 1.63 während zuvor die RMS-Werte um den Faktor 3.79 und die Pa(A)-Werte um den Faktor 4.89 unterschiedlich waren. Dafür streuen jetzt die Maximalwerte stärker (vorher 1.44, jetzt 3.13 bei RMS bzw. 4.12 bei Pa(A)-Anpassung).
Viel Spaß beim Ausprobieren der Pegelangleichung nach diesen Verfahren. Damit der Ärger über unterschiedliche Lautstärke von zusammengestellten CDs ein Ende hat . . .
Statistische Auswertung von 260 CD-Tracks
Um zu sehen, ob die Stücke unserer Hörtest-CD nicht allzu sehr aus dem Rahmen fallen haben wir mal andere Test-CDs und diverse Sampler analysiert, unter anderem:- Stereo-Test-CD 1-3
- Manger Test-CD
- Burmester Test-CD 3
- AndyNarell / SlowMotion (Jazz-Rock)
- Anastacia / NotThatKind (Pop)
- AlJarreau / AccentuateThePositive (Jazz-Pop)
- LarryCarlton / LastNite (Jazz-Blues)
- JohnnyAdams / OneFootInTheBlues (Blues)
- TinaTurner / PrivateDancer (Pop)
- DireStraits / BrothersInArms (Pop-Rock)
- Chesky / Jazz-Test-CD
- HiFi-Check CD
- Stereoplay-Test-CD
- KuschelBass (Bass-Effekt-CD)
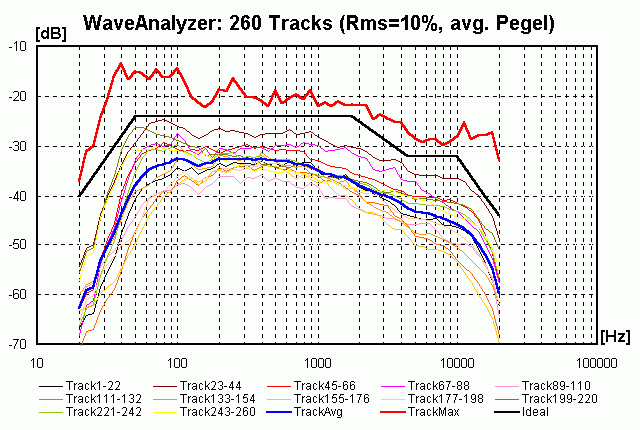
Der Maximalwert ist durch die breitere Streuung der Musikstile etwas höher als auf unserer Hörtest-CD (wieder auf einen RMS-Wert von 10% bezogen), außerdem sind die Extrembereiche (Bass < 50 Hz und Höhen > 10 kHz stärker vertreten. Die Überhöhung zwischen 400 und 1000 Hz zeigt sich hier aber auch:
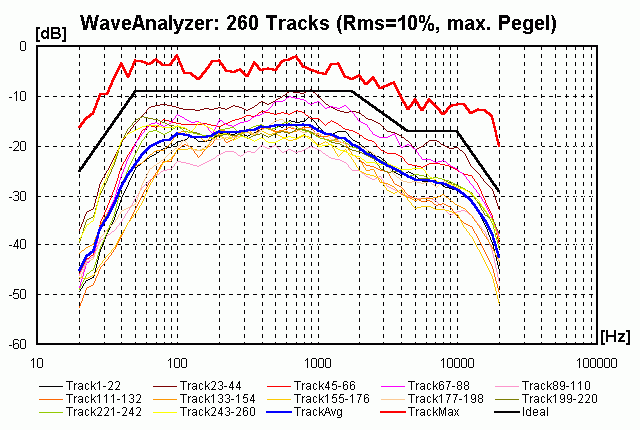
Extrembeispiele für Dynamikkompression:
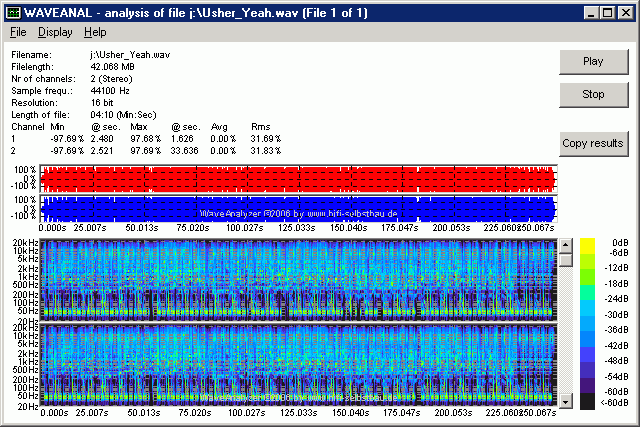
- Usher / Yeah (MP3-Ausschnitt, 44 kB):
massiver Einsatz von Dynamikkompression (Max/RMS = 3.08)
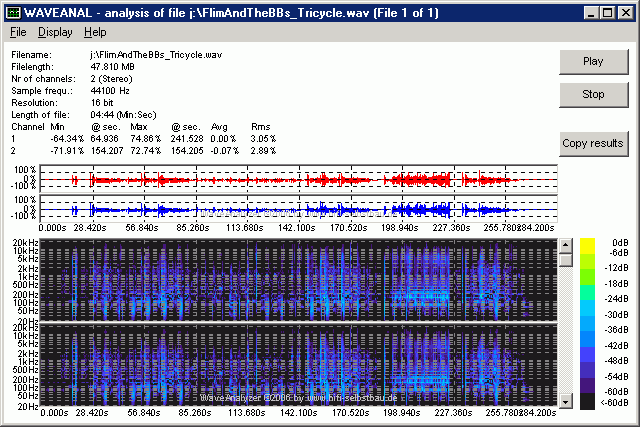
- Flim & the BBs / Tricycle (MP3-Ausschnitt, 95 kB):
extrem hohe Dynamik (Max/RMS = 24.5) -> bei gleicher subjektiver Lautstärke muss kurzzeitig die 10-fache Verstärkerspannung zur Verfügung stehen (Verhältnis der RMS-Werte 31.83 / 3.08), das entspricht der 100-fachen Verstärkerleistung! Das ist eine Härteprüfung für Verstärker und Lautsprecher!
Den Vergleich der Spektren ohne Ausgleich der unterschiedlichen RMS-Werte zeigt das folgende Bild:
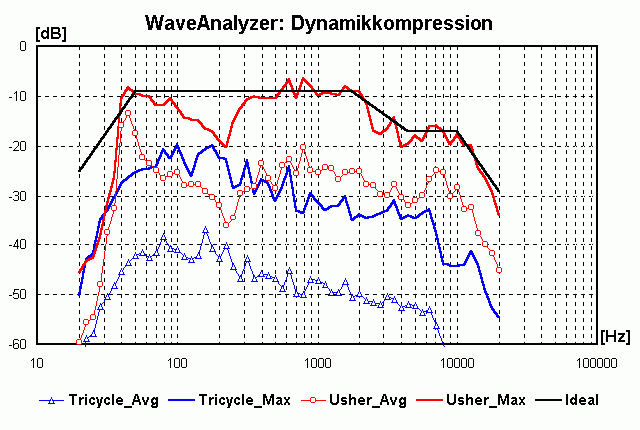
- Das Stück "Yeah" von Usher hat einen "Dauerbass" bei 42 Hz (Rms-Wert ist fast so hoch wie Max-Wert) und einen starken Einbruch bei 210 Hz (um das Dröhnen von PC-Subs und Kofferradios zu reduzieren und selbst dort den Eindruck von Tiefbass zu erzeugen). Außerdem ist die Überhöhung im Rms-Wert bei 7 kHz auffällig.
- Das Stück "Tricycle" hat ungewöhnlich viel Energie im Bereich 70 bis 250 Hz, muss daher bei den lauten Passagen her etwas warm klingen. Bei ungünstiger Raumakustik kann es dort schnell zuviel des Guten sein . . . Ab 6 kHz gibt es einen 10 dB "Erdrutsch" für die Höhen, auch dies trägt zum warmen Gesamtcharakter bei.
Zusammenfassung:
Auf die WAV-Dateien, fertig, los! Es gibt viel zu entdecken!